【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC=![]() ,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是__.
,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是__.
参考答案:
【答案】﹢1
【解析】
试题首先考虑到BE所在的三角形并不是特殊三角形,所以猜想到要求BE,可能需要构造直角三角形.由旋转的性质可知,AC=AE,∠CAE=60°,故△ACE是等边三角形,可证明△ABE与△CBE全等,可得到∠ABE=45°,∠AEB=30°,再证△AFB和△AFE是直角三角形,然后在根据勾股定理求解
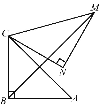
解:连结CE,设BE与AC相交于点F,如下图所示,
∵Rt△ABC中,AB=BC,∠ABC=90°
∴∠BCA=∠BAC=45°
∵Rt△ABC绕点A逆时针旋转60°与Rt△ADE重合,
∴∠BAC=∠DAE=45°,AC=AE
又∵旋转角为60°
∴∠BAD=∠CAE=60°,
∴△ACE是等边三角形
∴AC=CE=AE=4
在△ABE与△CBE中,![]()
∴△ABE≌△CBE (SSS)
∴∠ABE=∠CBE=45°,∠CEB=∠AEB=30°
∴在△ABF中,∠BFA=180°﹣45°﹣45°=90°
∴∠AFB=∠AFE=90°
在Rt△ABF中,由勾股定理得,
BF=AF=![]() =2
=2
又在Rt△AFE中,∠AEF=30,°∠AFE=90°
FE=AF=2
∴BE=BF+FE=2+2
故,本题的答案是:2+2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1) 请画出△ABC向左平移5个单位长度后得到的△A
 B
B C
C ;
;(2) 请画出△ABC关于原点对称的△A
 B
B C
C ;
;(3) 在
 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD⊥BC于点D,AE是∠BAC的平分线,∠B=30°,∠C=70°,分别求:

(1)∠BAC的度数;
(2)∠AED的度数;
(3)∠EAD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知下列命题中为真命题的是( )
①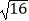 的算术平方根是4;
的算术平方根是4;
②若ma2>na2 , 则m>n;
③正八边形的一个内角的度数是135°;
④对角线互相垂直平分的四边形是菱形;
⑤平分弦的直径垂直于弦.
A.①③④
B.②③⑤
C.①④⑤
D.②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1所示,是由几个小立方块所搭几何体的俯视图,小立方块中的数字表示在该位置小立方块的个数.请画出从正面和从左面看到的这个几何体的形状图.(注意:画得不规范不给分)
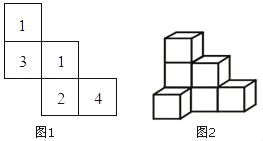
从正面看:
从左面看:
(2)如图2,一次数学活动课上,小明用7个棱长为1cm的小立方块积木搭成的几何体,然后他请小亮用尽可能少的同样大小的立方块在旁边再搭一个几何体,使小亮所搭的几何体恰好可以和小明所搭的几何体拼成一个大长方体(即拼大长方体时将其中一个几何体翻转,且假定组成每个几何体的立方块粘合在一起),则:
①小亮至少还需要 个小正方体;
②请画出小明所搭几何体的三视图,并计算①中小亮所搭几何体的表面积.
主视图:
俯视图:
左视图:
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了鼓励市民节约用水,万州市居民生活用水按阶梯式水价计费,表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信息:(水价计费
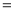 自来水销售费用
自来水销售费用 污水处理费用)
污水处理费用)自来水销售价格
污水处理价格
每户每月用水量
单价:元
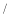 吨
吨单价:元
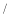 吨
吨17吨及以下
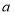
0.80
超过17吨不超过30吨的部分

0.80
超过30吨的部分
6.00
0.80
说明:①每户产生的污水量等于该户的用水量,②水费=自来水费+污水处理费;
已知小明家2013年3月份用水20吨,交水费66元;5月份用水25吨,交水费91元.
(1)求
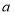 ,
, 的值.
的值.(2)随着夏天的到来,用水量将增加。为了节省开支,小梦计划把6月份的水费控制在不超过家庭月收入的2%,若小梦加的月收入为9200元,则小王家6月份最多能用水多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 经过点
经过点 ,
, .
.
(1)求直线
 的解析式;
的解析式;(2)若直线
 与直线
与直线 相交于点
相交于点 ,求点
,求点 的坐标;
的坐标;(3)根据图象,直接写出关于
 的不等式
的不等式 的解集.
的解集.
相关试题

