【题目】如图,OABC是平行四边形,对角线OB在轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=![]() 和y=
和y=![]() 的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①
的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①![]() ;②阴影部分面积是
;②阴影部分面积是![]() (k1+k2);③当∠AOC=90°时,|k1|=|k2|;④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是( )
(k1+k2);③当∠AOC=90°时,|k1|=|k2|;④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是( )

A.①②B.①④C.③④D.①②③
参考答案:
【答案】B
【解析】
作AE⊥y轴于点E,CF⊥y轴于点F,根据平行四边形的性质得S△AOB=S△COB,利用三角形面积公式得到AE=CF,则有OM=ON,再利用反比例函数k的几何意义和三角形面积公式得到S△AOM=![]() |k1|=
|k1|=![]() OMAM,S△CON=
OMAM,S△CON=![]() |k2|=
|k2|=![]() ONCN,所以有
ONCN,所以有![]() ;由S△AOM=
;由S△AOM=![]() |k1|,S△CON=
|k1|,S△CON=![]() |k2|,得到S阴影部分=S△AOM+S△CON=
|k2|,得到S阴影部分=S△AOM+S△CON=![]() (|k1|+|k2|)=
(|k1|+|k2|)=![]() (k1-k2);当∠AOC=90°,得到四边形OABC是矩形,由于不能确定OA与OC相等,则不能判断△AOM≌△CNO,所以不能判断AM=CN,则不能确定|k1|=|k2|;若OABC是菱形,根据菱形的性质得OA=OC,可判断Rt△AOM≌Rt△CNO,则AM=CN,所以|k1|=|k2|,即k1=-k2,根据反比例函数的性质得两双曲线既关于x轴对称,也关于y轴对称.
(k1-k2);当∠AOC=90°,得到四边形OABC是矩形,由于不能确定OA与OC相等,则不能判断△AOM≌△CNO,所以不能判断AM=CN,则不能确定|k1|=|k2|;若OABC是菱形,根据菱形的性质得OA=OC,可判断Rt△AOM≌Rt△CNO,则AM=CN,所以|k1|=|k2|,即k1=-k2,根据反比例函数的性质得两双曲线既关于x轴对称,也关于y轴对称.
作AE⊥y轴于E,CF⊥y轴于F,如图,
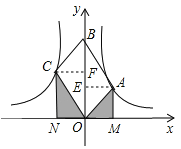
∵四边形OABC是平行四边形,
∴S△AOB=S△COB,
∴AE=CF,
∴OM=ON,
∵S△AOM=![]() |k1|=
|k1|=![]() OMAM,S△CON=
OMAM,S△CON=![]() |k2|=
|k2|=![]() ONCN,
ONCN,
∴![]() ,故①正确;
,故①正确;
∵S△AOM=![]() |k1|,S△CON=
|k1|,S△CON=![]() |k2|
|k2|
∴S阴影部分=S△AOM+S△CON=![]() (|k1|+|k2|),
(|k1|+|k2|),
而k1>0,k2<0,
∴S阴影部分=![]() (k1-k2),故②错误;
(k1-k2),故②错误;
当∠AOC=90°,
∴四边形OABC是矩形,
∴不能确定OA与OC相等,
而OM=ON,
∴不能判断△AOM≌△CNO,
∴不能判断AM=CN,
∴不能确定|k1|=|k2|,故③错误;
若OABC是菱形,则OA=OC,
而OM=ON,
∴Rt△AOM≌Rt△CNO,
∴AM=CN,
∴|k1|=|k2|,
∴k1=-k2,
∴两双曲线既关于x轴对称,也关于y轴对称,故④正确.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点(﹣1,y1),(2,y2),
 在反比例函数y=﹣
在反比例函数y=﹣ 的图象上,则下列关系式正确的是( )
的图象上,则下列关系式正确的是( )A.y3<y2<y1B.y2<y3<y1
C.y3<y1<y2D.y2<y1<y3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的外接圆为⊙O,点P在劣弧 CD上(不与C点重合).
(1)求∠BPC的度数;
(2)若⊙O的半径为8,求正方形ABCD的边长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某开发商准备开发建设一幢住宅区,工程需填土104米3,某工程队承包了该项填土任务.
(1)该工程队平均的填土量V(米3/天)与完成任务所需时间t(天)之间具有怎样的函数关系?
(2)该工程队共有10辆运输车,每辆车每天运土100米3,若工程必须在20天内完成任务,问:工程队每天至少派多少辆车运土,才能完成任务?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 在平面直角坐标系中.
在平面直角坐标系中.
(1)写出
 、
、 、
、 三点的坐标:
三点的坐标: ( ),
( ), ( ),
( ), ( );
( );(2)
 的面积为_______.
的面积为_______.(3)联结
 ,在平面直角坐标系中找一个点
,在平面直角坐标系中找一个点 ,使
,使 为等腰直角三角形,且以
为等腰直角三角形,且以 为直角边,则
为直角边,则 的坐标是________(直接写答案).
的坐标是________(直接写答案). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,四边形OABC是正方形,点A,C的坐标分别为(2,0),(0,2),D是x轴正半轴上的一点(点D在点A的右边),以BD为边向外作正方形BDEF(E,F两点在第一象限),连接FC交AB的延长线于点G.若反比例函数
 的图象经过点E,G两点,则k的值为 ______________.
的图象经过点E,G两点,则k的值为 ______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】4月23日是“世界读书日”,学校开展“让书香溢满校园”读书活动,以提升青少年的阅读兴趣,九年级(1)班数学活动小组对本年级600名学生每天阅读时间进行了统计,根据所得数据绘制了两幅不完整统计图(每组包括最小值不包括最大值).九年级(1)班每天阅读时间在0.5小时以内的学生占全班人数的8%.根据统计图解答下列问题:

(1)九年级(1)班有 名学生;
(2)补全直方图;
(3)除九年级(1)班外,九年级其他班级每天阅读时间在1~1.5小时的学生有165人,请你补全扇形统计图;
(4)求该年级每天阅读时间不少于1小时的学生有多少人.
相关试题

