【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下表(注:水费按月份结算,![]() 表示立方米):
表示立方米):
价目表 | |
每月用水量 | 单价 |
不超出 |
|
超出 |
|
超出 |
|
注:水费按月结算 | |
例:若某户居民![]() 月份用水
月份用水![]() ,应收水费为
,应收水费为![]() (元).
(元).
请根据上表的内容解答下列问题:
![]() 填空:若该户居民
填空:若该户居民![]() 月份用水
月份用水![]() ,则应收水费________元;
,则应收水费________元;
![]() 若该户居民
若该户居民![]() 月份用水
月份用水![]() (其中
(其中![]() ),则应收水费多少元?(用含
),则应收水费多少元?(用含![]() 的表示,并化简)
的表示,并化简)
![]() 若该户居民
若该户居民![]() ,
,![]() 两个月共用水
两个月共用水![]() (
(![]() 月份用水量超过了
月份用水量超过了![]() 月份),设
月份),设![]() 月份用水
月份用水![]() ,求该户居民
,求该户居民![]() ,
,![]() 两个月共交水费多少元?(用含
两个月共交水费多少元?(用含![]() 的表示,并化简)
的表示,并化简)
参考答案:
【答案】(1)8;(2)应收水费为![]() 元;(3)①
元;(3)①![]() 元;②
元;②![]() 月份用水量不少于
月份用水量不少于![]() 但不超过
但不超过![]() ③
③![]() (元)
(元)
【解析】
(1)不超过6m3,单价为2元.水费=单价×数量;
(2)水费=单价为2元的6m3的水费+单价为4元的超过6m3的水费;
(3)应分情况讨论:4月份不超过6m3,5月份10立方米以上;或4月份不超过6m3,5月份在6-10立方米之间;两个月都在6-10立方米之间.
解:(1)![]() (元);
(元);
(2)![]() ,
,
∴应收水费为![]() 元.
元.
![]() 因为
因为![]() 月份用水量超过了
月份用水量超过了![]() 月份,所以
月份,所以![]() 月份用水量少于
月份用水量少于![]() .
.
①当![]() 月份用水量少于
月份用水量少于![]() 时,则
时,则![]() 月份用水量超过
月份用水量超过![]() ,
,
∴![]() ,
,![]() 两个月共交水费
两个月共交水费![]() (元);
(元);
②当![]() 月份用水量大于或等于
月份用水量大于或等于![]() 但不超过
但不超过![]() 时,则
时,则![]() 月份用水量不少于
月份用水量不少于![]() 但不超过
但不超过![]() ,
,
∴![]() 、
、![]() 两个月共交水费
两个月共交水费![]() (元);
(元);
③当![]() 月份用水量超过
月份用水量超过![]() 但少于
但少于![]() 时,则
时,则![]() 月份用水量超过
月份用水量超过![]() 但少于
但少于![]() ,
,
∴![]() ,
,![]() 两个月共交水费
两个月共交水费![]() (元).
(元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】用单项式表示下列各式,并指出其系数和次数.
 王明同学买
王明同学买 本练习册花
本练习册花 元,那么买
元,那么买 本练习册要花多少元?
本练习册要花多少元? 正方体的棱长为
正方体的棱长为 ,那么它的表面积是多少?体积呢?
,那么它的表面积是多少?体积呢? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将两个完全相同的三角形纸片ABC和A′B′C重合放置,其中∠C=90°,∠B=∠B′=30°,AC=AC′=2.
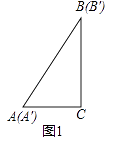
(1)如图2,固定△ABC,将△A′B′C绕点C旋转,当点A′恰好落在AB边上时,
①∠CA′B′=;旋转角ɑ=(0°<ɑ<90°),线段A′B′与AC的位置关系是;
(2)②设△A′BC的面积为S1 , △AB′C的面积为S2 , 则S1与S2的数量关系是什么?证明你的结论;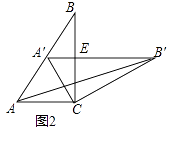
(3)如图3,∠MON=60°,OP平分∠MON,OP=PN=4,PQ∥MO交ON于点Q.若在射线OM上存在点F,使S△PNF=S△OPQ , 请直接写出相应的OF的长.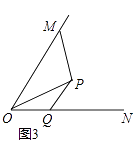
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016.镇江)如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°.
(1)若∠ABC=35°,求∠CAO的度数;
(2)求证:CO=DO

-
科目: 来源: 题型:
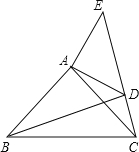
查看答案和解析>>【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,AB>AC,BE,CF都是△ABC的高线,P是BE上一点,且BP=AC,Q是CF延长线上一点,且CQ=AB,连结AP,AQ,QP.求证:
(1)AQ=PA.
(2)AP⊥AQ.

-
科目: 来源: 题型:
查看答案和解析>>【题目】数学家高斯在上学时曾经研究过这样一个问题,
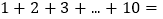 ?
?经过研究,这个问题的一般性结论是
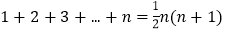 ,其中
,其中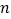 为正整数,现在我们来研究一个类似的问题:
为正整数,现在我们来研究一个类似的问题: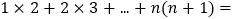 ?
?观察下面三个特殊的等式:


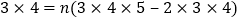
将这三个等式的两边相加,可以得到
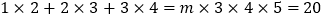 .
.读完这段材料,请你计算:
(1)
 ________;(直接写出结果)
________;(直接写出结果)(2)
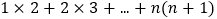 ;(写出计算过程)
;(写出计算过程)(3)
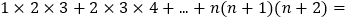 ________.
________.
相关试题

