【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
A.a>0
B.3是方程ax2+bx+c=0的一个根
C.a+b+c=0
D.当x<1时,y随x的增大而减小
参考答案:
【答案】B
【解析】解:A、因为抛物线开口向下,因此a<0,故此选项错误;
B、根据对称轴为x=1,一个交点坐标为(﹣1,0)可得另一个与x轴的交点坐标为(3,0)因此3是方程ax2+bx+c=0的一个根,故此选项正确;
C、把x=1代入二次函数y=ax2+bx+c(a≠0)中得:y=a+b+c,由图象可得,y>0,故此选项错误;
D、当x<1时,y随x的增大而增大,故此选项错误;
所以答案是:B.
【考点精析】根据题目的已知条件,利用二次函数的性质和二次函数图象以及系数a、b、c的关系的相关知识可以得到问题的答案,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店进行店庆活动,决定购进甲、乙两种纪念品,若购进甲种纪念品1件,乙种纪念品2件,需要160元;购进甲种纪念品2件,乙种纪念品3件,需要280元.
(1)购进甲乙两种纪念品每件各需要多少元?
(2)该商场决定购进甲乙两种纪念品100件,并且考虑市场需求和资金周转,用于购买这些纪念品的资金不少于6300元,同时又不能超过6430元,则该商场共有几种进货方案?
(3)若销售每件甲种纪念品可获利30元,每件乙种纪念品可获利12元,在第(2)问中的各种进货方案中,哪种方案获利最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知 AD⊥BC,垂足为点 D,EF⊥BC,垂足为点 F,∠1+∠2=180°, 请填写∠CGD=∠CAB 的理由.

解:因为 AD⊥BC,EF⊥BC( )
所以∠ADC=90°,∠EFD=90°( )
得∠ADC=∠EFD( )
所以 AD//EF( )
得∠2+∠3=180° ( )
又因为∠1+∠2=180°(已知)
所以∠1=∠3( )
所以 DG//AB( )
所以∠CGD=∠CAB( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果点P(2x+6,x-4)在平面直角坐标系的第四象限内,那么x的取值范围在数轴上可表示为
A.
 B.
B.  C.
C. 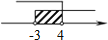 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某高校共有5个大餐厅和2个小餐厅。经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐。
(1)1个大餐厅和1个小餐厅分别可供多少名学生就餐?
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数与反比例的图象相交于A、B两点,则图中使反比例函数的值小于一次函数的值的x的取值范围是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=6,BC=8,AC,BD相交于O,P是边BC上一点,AP与BD交于点M,DP与AC交于点N.
①若点P为BC的中点,则AM:PM=2:1;
②若点P为BC的中点,则四边形OMPN的面积是8;
③若点P为BC的中点,则图中阴影部分的总面积为28;
④若点P在BC的运动,则图中阴影部分的总面积不变.
其中正确的是 . (填序号即可)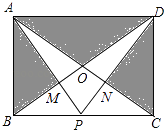
相关试题

