【题目】如图,矩形ABCD中,AB=10,BC=5,点P为AB边上一动点(不与点A,B重合),DP交AC于点Q.
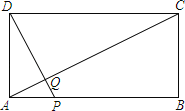
(1)求证:△APQ∽△CDQ;
(2)当PD⊥AC时,求线段PA的长度;
(3)当点P在线段AC的垂直平分线上时,求sin∠CPB的值.
参考答案:
【答案】(1)见解析;(2)AP=![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)根据矩形的性质和相似三角形的判定定理证明即可;
(2)根据垂直的定义、相似三角形的性质列出比例式,计算即可;
(3)连接PC,根据线段垂直平分线的性质得到PC=PA,设PA=x,根据勾股定理列出关于x的方程,解方程即可.
(1)证明:∵四边形ABCD是矩形,
∴DC∥AB,
∴∠QAP=∠QCD,∠QPA=∠QDC,
∴△APQ∽△CDQ;
(2)解:∵PD⊥AC,
∴∠QDC+∠QCD=90°,又∠QDC+∠QDA=90°,
∴∠QCD=∠QDA,又∠DAP=∠CDA=90°,
∴△DAP∽△CDA,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,AP=![]() ;
;
(3)解:连接PC,
∵点P在线段AC的垂直平分线上,
∴PC=PA,
设PA=x,则PC=x,PB=10﹣x,
由勾股定理得,PC2=PB2+BC2,即x2=(10﹣x)2+25,
解得,x=![]() ,
,
∴PC=PA=![]() ,
,
∴sin∠CPB=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等式(x+4)0=1成立的条件是( )
A.x为有理数 B.x≠0 C.x≠4 D.x≠-4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果x+4y﹣3=0,那么2x16y= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了开阔学生的视野,积极组织学生参加课外读书活动.“放飞梦想”读书小组协助老师随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他等四类),并将调查结果绘制成如下两幅不完整的统计图,请你结合图中的信息解答下列问题:
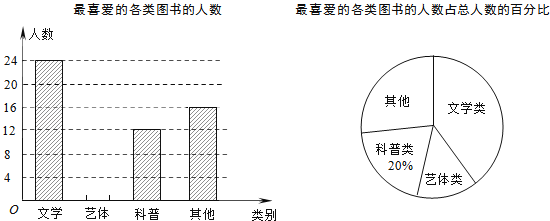
(1)求被调查的学生人数;
(2)补全条形统计图;
(3)已知该校有1200名学生,估计全校最喜爱文学类图书的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】月球距离地球约为3.84×105千米,一架飞机速度为8×102千米/时,若坐飞机飞行这么远的距离需 _________ 小时
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明命题:“若a,b是整数,ab能被3整除,那么a,b中至少有一个能被3整除”时,假设应为( )
A. a,b都能被3整除 B. a不能被3整除 C. a,b不都能被3整除 D. a,b都不能被3整除
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中,成比例的是( )
A. -6,-8,3,4 B. -7,-5,14,5 C. 3,5,9,12 D. 2,3,6,12
相关试题

