【题目】两组邻边分别相等的四边形叫做筝形.如图1,四边形ABCD是一个筝形,其中AD=CD,AB=CB,我们称这个四边形是“筝形ABCD”.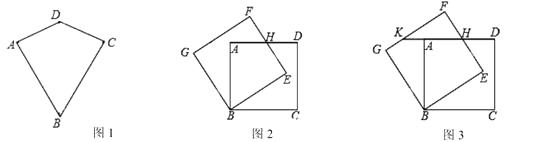
(1)根据筝形的定义判断下列命题是否正确,真命题打“√”,假命题打“×”.
①筝形有一组对角相等.
②菱形是筝形.
③筝形的面积为两条对角线长度的乘积.
(2)如图2,有一个公共顶点B的两个正方形ABCD与正方形BEFG全等,边AD与EF相交于点H.请你判断四边形BEHA是否是“筝形”,说明你的理由;
(3)如图3,当∠EBC=30°时,延长DA交GF于点K.若正方形ABCD边长为 ![]() ,求线段AK的长.
,求线段AK的长.
参考答案:
【答案】
(1)√;√;×
(2)
解:是.理由:连接BH,
∵两个正方形ABCD与正方形BEFG全等,
∴AB=BE,∠A=∠E=90°,
在Rt△ABH和△EBH中,
![]()
Rt△ABHRt△EBH,
∴AH=EH.
∴四边形BEHA是筝形.
(3)
解:∵Rt△ABHRt△EBH,
∴∠ABH=∠EBH,
∵∠EBC=30°,∴∠ABE=60°,∴∠ABH=∠EBH=30°,∠AHE=120°,
∴∠KHF=60°.
在Rt△BEH中,∠EBH=30°,则HE= ![]() BE=1;
BE=1;
则FH= ![]() .
.
在Rt△KFH中,∠KFH=60°,则KH=2FH= ![]() .
.
【解析】解:(1)①真命题,例如图1中∠A=∠C;
②真命题,菱形的四条边相等,是一种特殊的筝形;
③假命题,筝形两条对角线是互相垂直的,则它的面积为两对角线之积的一半;
【考点精析】掌握含30度角的直角三角形是解答本题的根本,需要知道在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】由于雾霾天气趋于严重,我市某电器商城根据民众健康需求,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)完成下列表格,并直接写出月销售量y(台)与售价x(元/台)之间的函数关系式及售价x的取值范围;
售价(元/台)
月销售量(台)
400
200
250
x
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解题:
你知道为什么任何无限循环小数都可以写成分数形式吗?下面的解答过程会告诉你原因和方法.
(1)阅读下列材料:
问题:利用一元一次方程将
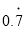 化成分数.
化成分数.设
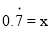 .
.由
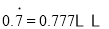 ,可知
,可知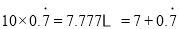 ,
,即
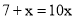 .(请你体会将方程两边都乘以10起到的作用)
.(请你体会将方程两边都乘以10起到的作用)可解得
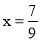 ,即
,即 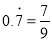 .
.填空:将
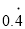 直接写成分数形式为_____________ .
直接写成分数形式为_____________ .(2)请仿照上述方法把小数
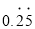 化成分数,要求写出利用一元一次方程进行解答的过程.
化成分数,要求写出利用一元一次方程进行解答的过程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=30°,求∠DOE的度数;
(2)在图①中,若∠AOC=
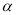 ,直接写出∠DOE的度数(用含
,直接写出∠DOE的度数(用含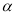 的代数式表示);
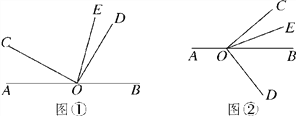
的代数式表示);(3)将图①中的∠DOC绕顶点O顺时针旋转至图②的位置,探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面内,∠A的两边分别与∠B的两边平行,且∠A比∠B的3倍少40°,则∠A =_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中正确的是( )
A. 22=(-2)2B. 33=(-3)3C. -22=|-22 |D. -33=|33 |
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点M(﹣2,3)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
相关试题

