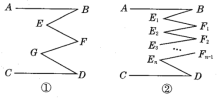
【题目】(1)如图1,AB∥CD,则∠E+∠G与∠B+∠F+∠D有何关系?
(2)如图2,若AB∥CD,又能得到什么结论?请直接写出结论.
参考答案:
【答案】(1) ∠E+∠G=∠B+∠F+∠D;
(2) ∠B+∠F1+∠F2+…+∠Fn-1+∠D=∠E1+∠E2+…+∠En.
【解析】
(1)过点E作EM∥AB,过点F作FN∥AB,过点G作GH∥CD,根据平行线的性质可得答案;
(2) 根据平行线的性质易得:∠B+∠F1+∠F2+…+∠Fn-1+∠D=∠E1+∠E2+…+∠En.
解:(1)过点E作EM∥AB,过点F作FN∥AB,过点G作GH∥CD.
∵AB∥CD.
∴AB∥EM∥FN∥GH∥CD.
∴∠1=∠B,∠2=∠3,∠4=∠5,∠6=∠D.
∴∠1+∠2+∠5+∠6=∠B+∠3+∠4+∠D,
即∠BEF+,∠FGD=∠B+∠EFG+∠D.
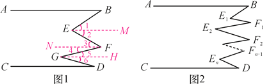
(2)∠B+∠F1+∠F2+…+∠Fn-1+∠D=∠E1+∠E2+…+∠En.
-
科目: 来源: 题型:
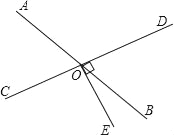
查看答案和解析>>【题目】如图,AB和CD相交于点O,∠DOE=90°,若∠BOE=
 ∠AOC,
∠AOC,(1)指出与∠BOD相等的角,并说明理由.
(2)求∠BOD,∠AOD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD丄AC 于D,EF丄AC 于F.∠AMD=∠AGF.∠1=∠2=35°
(1)求∠GFC的度数:
(2)求证:DM∥BC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=_______度;
(2)如图2如果∠BAC=60°,则∠BCE=______度;
(3)设∠BAC=
 ,∠BCE=
,∠BCE= .
.①如图3,当点D在线段BC上移动,则
 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;②当点D在直线BC上移动,请直接写出
 之样的数量关系,不用证明。
之样的数量关系,不用证明。



-
科目: 来源: 题型:
查看答案和解析>>【题目】填写推理理由,将过程补充完整:
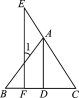
如图,已知AD⊥BC于点D,EF⊥BC于点F,AD平分∠BAC.求证:∠E=∠1.
证明:∵AD⊥BC,EF⊥BC(已知),
∴∠ADC=∠EFC=90°(垂直的定义).
∴____________(_____________).
∴∠1=_____(_____________),
∠E=_____(_______________).
又∵AD平分∠BAC(已知),
∴_____=________.
∴∠1=∠E(等量代换).
-
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时
 张用A方法,其余用B方法。
张用A方法,其余用B方法。(1)用
 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料,解答后面的问题.
解方程:
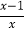 -
-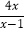 =0.
=0.解:设y=
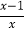 ,则原方程可化为y-
,则原方程可化为y-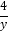 =0,方程两边同时乘y,得y2-4=0,解得y1=2,y2=-2.
=0,方程两边同时乘y,得y2-4=0,解得y1=2,y2=-2.经检验,y1=2,y2=-2都是方程y-
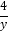 =0的解.
=0的解.当y=2时,
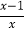 =2,解得x=-1;当y=-2时,
=2,解得x=-1;当y=-2时,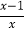 =-2,解得x=
=-2,解得x= .
.经检验,x1=-1,x2=
 都是原分式方程的解.所以原分式方程的解为x1=-1,x2=
都是原分式方程的解.所以原分式方程的解为x1=-1,x2= .
.上述这种解分式方程的方法称为换元法.
问题:
(1)若在方程
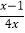 -
-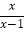 =0中,设y=
=0中,设y=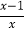 ,则原方程可化为________________;
,则原方程可化为________________;(2)若在方程
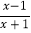 -
-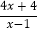 =0中,设y=
=0中,设y=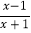 ,则原方程可化为________________;
,则原方程可化为________________;(3)模仿上述换元法解方程:
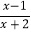 -
-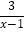 -1=0.
-1=0.
相关试题

