【题目】如图,点D、E分别是边AB、AC的中点,将△ADE沿着DE对折,点A落在BC边上的点F,若∠B=50°,则∠BDF的度数为( ) 
A.50°
B.70°
C.75°
D.80°
参考答案:
【答案】D
【解析】解:∵点D、E分别边AB、AC的中点, ∴DE是△ABC的中位线,
∴DE∥BC,
∴∠ADE=∠B=50°,
∵△DEF是△DEA经过翻折变换得到的,
∴∠EDF=50°,
∴∠BDF=180°﹣2∠ADE=180°﹣100°=80°.
故选:D.
【考点精析】根据题目的已知条件,利用三角形的内角和外角和三角形中位线定理的相关知识可以得到问题的答案,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.
-
科目: 来源: 题型:
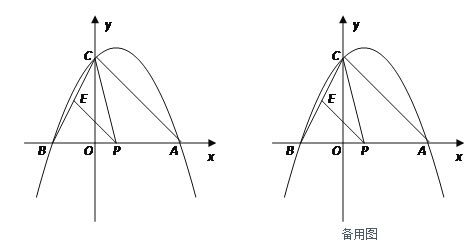
查看答案和解析>>【题目】如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1>x2,与y轴交于点C(0,4),其中x1、x2是方程x2-2x-8=0的两个根.
(1)求这条抛物线的解析式;
(2)点P是线段AB上的动点,过点P作PE∥AC,交BC于点E,连接CP,当△CPE的面积最大时,求点P的坐标;
(3)探究:若点Q是抛物线对称轴上的点,是否存在这样的点Q,使△QBC成为等腰三角形?若存在,请直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)
(参考数据:sin48°≈
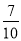 ,tan48°≈
,tan48°≈ ,sin64°≈
,sin64°≈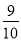 ,tan64°≈2)
,tan64°≈2)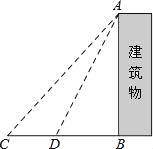
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
(1)求证:∠BDC=∠A;
(2)若CE=4,DE=2,求AD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是重叠的两个直角三角形.将其中一个直角三角形沿BC方向平移得到△DEF.如果AB=8cm,BE=4cm,DH=3cm,则图中阴影部分面积为cm2 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】用四舍五入法按要求对3.1415926分别取近似值,其中错误的是( )
A. 3.1(精确到0.1) B. 3.141(精确到千分位)
C. 3.14(精确到百分位) D. 3.1416(精确到0.0001)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB =90°,∠ABC=30°,将△ABC绕点C顺时针旋转
 角(0°<
角(0°<  <180°)至△A′B′C , 使得点A′恰好落在AB边上,则
<180°)至△A′B′C , 使得点A′恰好落在AB边上,则  等于( ).
等于( ).
A.150°
B.90°
C.60°
D.30°
相关试题

