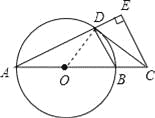
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
(1)求证:∠BDC=∠A;
(2)若CE=4,DE=2,求AD的长.

参考答案:
【答案】(1)证明过程见解析;(2)6.
【解析】试题分析:(1)连接OD,由CD是⊙O切线,得到∠ODC=90°,根据AB为⊙O的直径,得到∠ADB=90°,等量代换得到∠BDC=∠ADO,根据等腰直角三角形的性质得到∠ADO=∠A,即可得到结论;(2)根据垂直的定义得到∠E=∠ADB=90°,根据平行线的性质得到∠DCE=∠BDC,根据相似三角形的性质得到![]() ,解方程即可得到结论.
,解方程即可得到结论.
试题解析:(1)连接OD, ∵CD是⊙O切线, ∴∠ODC=90°, 即∠ODB+∠BDC=90°,
∵AB为⊙O的直径, ∴∠ADB=90°, 即∠ODB+∠ADO=90°, ∴∠BDC=∠ADO,
∵OA=OD, ∴∠ADO=∠A, ∴∠BDC=∠A;
(2)∵CE⊥AE, ∴∠E=∠ADB=90°, ∴DB∥EC, ∴∠DCE=∠BDC, ∵∠BDC=∠A, ∴∠A=∠DCE,
∵∠E=∠E, ∴△AEC∽△CED, ∴![]() , ∴EC2=DEAE, ∴16=2(2+AD), ∴AD=6.
, ∴EC2=DEAE, ∴16=2(2+AD), ∴AD=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x+y=4,xy=2,试求下列各式的值:
(1)x2+y2;
(2)x4+y4.
-
科目: 来源: 题型:
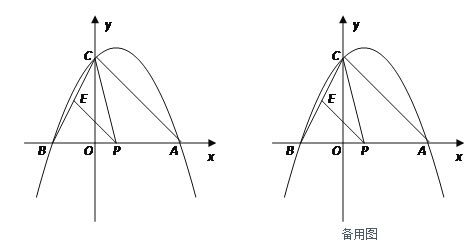
查看答案和解析>>【题目】如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1>x2,与y轴交于点C(0,4),其中x1、x2是方程x2-2x-8=0的两个根.
(1)求这条抛物线的解析式;
(2)点P是线段AB上的动点,过点P作PE∥AC,交BC于点E,连接CP,当△CPE的面积最大时,求点P的坐标;
(3)探究:若点Q是抛物线对称轴上的点,是否存在这样的点Q,使△QBC成为等腰三角形?若存在,请直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)
(参考数据:sin48°≈
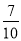 ,tan48°≈
,tan48°≈ ,sin64°≈
,sin64°≈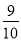 ,tan64°≈2)
,tan64°≈2)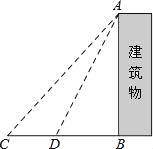
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D、E分别是边AB、AC的中点,将△ADE沿着DE对折,点A落在BC边上的点F,若∠B=50°,则∠BDF的度数为( )

A.50°
B.70°
C.75°
D.80° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是重叠的两个直角三角形.将其中一个直角三角形沿BC方向平移得到△DEF.如果AB=8cm,BE=4cm,DH=3cm,则图中阴影部分面积为cm2 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】用四舍五入法按要求对3.1415926分别取近似值,其中错误的是( )
A. 3.1(精确到0.1) B. 3.141(精确到千分位)
C. 3.14(精确到百分位) D. 3.1416(精确到0.0001)
相关试题

