【题目】如图,以![]() 的三边为边分别作等边
的三边为边分别作等边![]() 、
、![]() 、
、![]() ,则下列结论:①①
,则下列结论:①①![]() ;②四边形
;②四边形![]() 为平行四边形;③当
为平行四边形;③当![]() 时,四边形
时,四边形![]() 是菱形;④当
是菱形;④当![]() 时,四边形
时,四边形![]() 是矩形.其中正确的结论有( )个.
是矩形.其中正确的结论有( )个.

A. 1 B. 2 C. 3 D. 4
参考答案:
【答案】C
【解析】
①由△ABE与△BCF都为等边三角形,利用等边三角形的性质得到两对边相等,∠ABE=∠CBF=60°,利用等式的性质得到夹角相等,利用SAS得到△EBF与△DFC全等;
②利用(1)中全等三角形对应边相等得到EF=AC,再由三角形ADC为等边三角形得到三边相等,等量代换得到EF=AD,AE=DF,利用对边相等的四边形为平行四边形得到AEFD为平行四边形;
③当AE=AD时,ADFE是菱形,可以用邻边相等的平行四边形是菱形判断即可;
④当∠BAC=150°,由此可求得∠EAD的度数,则可得ADFE是矩形,由此即可判断;
∵△ABE、△BCF为等边三角形,
∴AB=BE=AE,BC=CF=FB,∠ABE=∠CBF=60°,
∴∠ABE∠ABF=∠FBC∠ABF,即∠CBA=∠FBE,
在△ABC和△EBF中,
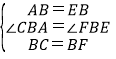 ,
,
∴△ABC≌△EBF(SAS),
∴EF=AC,
又∵△ADC为等边三角形,
∴CD=AD=AC,
∴EF=AD=DC,
同理可得△ABC≌△DFC,
∴DF=AB=AE=DF,
∴四边形AEFD是平行四边形;
∴∠FEA=∠ADF,
∴∠FEA+∠AEB=∠ADF+∠ADC,即∠FEB=∠CDF,
在△FEB和△CDF中,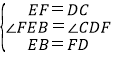 ,
,
∴△EBF≌△DFC(SAS),故①正确,
∴EB=DF,EF=DC.
∵△ACD和△ABE为等边三角形,
∴AD=DC,AE=BE,
∴AD=EF,AE=DF
∴四边形AEFD是平行四边形;故②正确,
若AB=AC,则AE=AD,四边形AEFD是菱形此,
故△ABC满足AB=AC时,四边形AEFD是菱形;故③正确;
若∠BAC=90°,则平行四边形AEFD是矩形;
由(1)知四边形AEFD是平行四边形,则∠EAD=90°时,可得平行四边形AEFD是矩形,
∴∠BAC=360°60°60°90°=150°,
即△ABC满足∠BAC=150°时,四边形AEFD是矩形;
∴∠BAC=90°,四边形AEFD不是矩形;故④错误,
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)(x-5)2=16 (直接开平方法) (2)x2+5x=0 (因式分解法)
(3)x2-4x+1=0 (配方法) (4)x2+3x-4=0 (公式法)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,
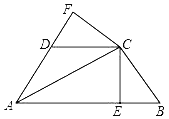
(1)求证:△BCE≌△DCF;
(2)若AB=21,AD=9,BC=CD=10,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】销售某种商品,根据经验,销售单价不少于30元 /件,但不超过50元 /件时,销售数量N (件)与商品单价M (元 /件)的函数关系的图象如图所示中的线段AB.

(1)求y关于x的函数关系式;
(2)如果计划每天的销售额为2400元时,那么该商品的单价应该定多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD中AD∥BC,边AB=4,BC=8.将此长方形沿EF折叠,使点D与点B重合,点C落在点G处.
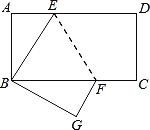
(1)试判断△BEF的形状,并说明理由;
(2)若AE=3,求△BEF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,李老师出示了如下框中的题目.
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由.
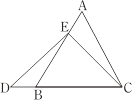
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).

图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
 中,
中, 为对角线,
为对角线, 为
为 上一点,连接
上一点,连接 ,
, ,
, 的延长线交
的延长线交 于点
于点 ,
, ,则
,则 的度数为________.
的度数为________.
相关试题

