【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的三个顶点的坐标分别是:A(2,2),B(1,0),C(3,1).
(1)画出△ABC关于x轴对称的△A′B′C′,并求出点A′、B′、C′的坐标.
(2)在坐标平面内是否存在点D,使得△COD为等腰三角形?若存在,直接写出点D的坐标(找出满足条件的两个点即可);若不存在,请说明理由.

参考答案:
【答案】(1)画图见解析,![]() (2,-2),
(2,-2),![]() (1,0),
(1,0),![]() (3,-1)
(3,-1)
(2)存在点D使得△COD为等腰三角形,
满足条件的点D在坐标轴上的坐标.D1(6,0);D2(![]() ,0);D3(
,0);D3(![]() ,0);D4(-
,0);D4(-![]() ,0);D5(0,5);D6(0,
,0);D5(0,5);D6(0,![]() );D7(0,2);D8(0,-
);D7(0,2);D8(0,-![]() );(答案不唯一,正确即可得分)
);(答案不唯一,正确即可得分)
【解析】
试题(1)按照条件画出即可,并根据关于X轴对称的点的特点写出点的坐标
(2)只要是线段OC垂直平分线上的点均满足条件,这样的点有很多
试题解析:(1)如图△![]() 即为所做的三角形.
即为所做的三角形.
其中![]() (2,-2),
(2,-2),![]() (1,0),
(1,0),![]() (3,-1).
(3,-1).
(2)存在点D使得△COD为等腰三角形,(答案不唯一,正确即可得分)
提示:如图所示,满足条件的点D在坐标轴上的坐标.D1(6,0);D2(![]() ,0);D3(
,0);D3(![]() ,0);D4(-
,0);D4(-![]() ,0);D5(0,5);D6(0,
,0);D5(0,5);D6(0,![]() );D7(0,2);D8(0,-
);D7(0,2);D8(0,-![]() );或垂直平分线
);或垂直平分线![]() 上任一点即可.
上任一点即可.


-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理(解析)
提出问题:如图1,在四边形ABCD中,P是AD边上任意一点,△PBC与△ABC和△DBC的面积之间有什么关系?探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
当AP=
 AD时(如图2):
AD时(如图2):∵AP=
 AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,∴S△ABP=
 S△ABD,
S△ABD,∵PD=AD﹣AP=
 AD,△CDP和△CDA的高相等
AD,△CDP和△CDA的高相等∴S△CDP=
 S△CDA,
S△CDA,∴S△PBC=S四边形ABCD﹣S△ABP﹣S△CDP=S四边形ABCD﹣
 S△ABD﹣
S△ABD﹣ S△CDA,
S△CDA,=S四边形ABCD﹣
 (S四边形ABCD﹣S△DBC)﹣
(S四边形ABCD﹣S△DBC)﹣ (S四边形ABCD﹣S△ABC)=
(S四边形ABCD﹣S△ABC)= S△DBC+
S△DBC+ S△ABC.
S△ABC.(1)当AP=
 AD时,探求S△PBC与S△ABC和S△DBC之间的关系式并证明;
AD时,探求S△PBC与S△ABC和S△DBC之间的关系式并证明;(2)当AP=
 AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;
AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;(3)一般地,当AP=
 AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系为: ;
AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系为: ;(4)当AP=
 AD(0≤
AD(0≤ ≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .
≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角梯形
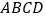 中,
中, ,
, 为
为 边上一点,
边上一点, ,且
,且 .连接
.连接 交对角线
交对角线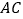 于
于 ,连接
,连接 .下列结论:
.下列结论:
①
 ;②
;② 为等边三角形;
为等边三角形;③
 ; ④
; ④ .其中结论正确的是
.其中结论正确的是A.只有①②
B.只有①②④
C.只有③④
D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车间有技术工人85人,平均每天每人可加工甲种部件16个或乙种部件10个,2个甲种部件和3个乙种部件配成一套,问加工甲、乙两种部件各安排多少人才能使每天加工的两种部件刚好配套?并求出加工了多少套?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
-
科目: 来源: 题型:
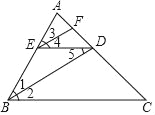
查看答案和解析>>【题目】如图,BD是∠ABC的平分线,ED∥BC,∠4=∠5,则EF也是∠AED的平分线.完成下列推理过程:
证明:∵BD是∠ABC的平分线(已知)
∴∠1=∠2(角平分线定义)
∵ED∥BC(已知)
∴∠5=∠2( )
∴∠1=∠5(等量代换)
∵∠4=∠5(已知)
∴EF∥ ( )
∴∠3=∠1( )
∴∠3=∠4(等量代换)
∴EF是∠AED的平分线(角平分线定义)
-
科目: 来源: 题型:
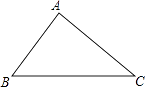
查看答案和解析>>【题目】如图,在△ABC中,BC=10,∠B=60°,∠C=45°,则点A到BC的距离是( )
A.10﹣5
B.5+5
C.15﹣5
D.15﹣10
相关试题

