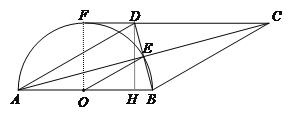
【题目】四边形ABCD的对角线交于点E,有AE=EC,BE=ED,以AB为直径的半圆过点E,圆心为O.

(1)利用图1,求证:四边形ABCD是菱形.
(2)如图2,若CD的延长线与半圆相切于点F,已知直径AB=8.
①连结OE,求△OBE的面积.
②求弧AE的长.
参考答案:
【答案】(1)证明见解析;(2)①4,②p.
【解析】试题分析: (1)利用对角线互相平分可先判断四边形ABCD为平行四边形,再利用直径对的圆周角是90°可得到AC⊥BD,就可判断是菱形.(2)①连接OF,可得OF为△ABD边AB上的高,可求得△ABD的面积为16,△AEB面积为△ABD的面积的一半,即等于8,△OEB的面积为△AEB面积的一半,即等于4;④过点D作DH⊥AB于点H.可得四边形OFDH为矩形,在Rt△ADH中利用三角函数可求得∠DAH=30°,进而可求得∠AOE的度数,弧AE的长度可求.
试题解析:(1)∵AE="EC,BE=ED," ∴四边形ABCD是平行四边形.∵AB为直径,且过点E,∴∠AEB=90°,即AC⊥BD.而四边形ABCD是平行四边形,∴四边形ABCD是菱形.(2)①连结OF.∵CD的延长线与半圆相切于点F,∴OF⊥CF.∵FC∥AB,∴OF即为△ABD的AB边上的高.S△ABD=AB×OF=×8×4=16.∵点O,E分别是AB,BD的中点,∴S△ABE=S△ABD=8,所以,S△OBE=S△ABE=4.②过点D作DH⊥AB于点H.∵AB∥CD,OF⊥CF,
∴FO⊥AB,∴∠F=∠FOB=∠DHO=90°.∴四边形OHDF为矩形,即DH=OF=4.在Rt△DAH中,sin∠DAB=![]() =,∴∠DAH=30°.∵点O,E分别为AB,BD中点,∴OE∥AD,∴∠EOB=∠DAH=30°.∴∠AOE=180°-∠EOB=150°.∴弧AE的长=
=,∴∠DAH=30°.∵点O,E分别为AB,BD中点,∴OE∥AD,∴∠EOB=∠DAH=30°.∴∠AOE=180°-∠EOB=150°.∴弧AE的长=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个不相等的角互为补角,那么这两个角 ( )
A.都是锐角B.都是钝角C.一个锐角,一个钝角D.以上答案都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在4×5网格图中,其中每个小正方形边长均为1,梯形ABCD和五边形EFGHK的顶点均为小正方形的顶点.
(1)以B为位似中心,在网格图中作四边形A′BC′D′,使四边形A′BC′D′和梯形ABCD位似,且位似比为2:1;
(2)求(1)中四边形A′BC′D′与五边形EFGHK重叠部分的周长.(结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个角的补角等于这个角的余角的4倍,求这个角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=(k﹣3)x+2k﹣8
(1)若一次函数的图象经过原点,求k的值;
(2)若一次函数的图象与直线y=2x+1平行,求k的值;
(3)若一次函数y的值随x的值的增大而减小,求k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们都知道“三角形的内角和等于180°”。如图1,教材中是用“延长BC,过点C作CE∥AB”的方法把∠A移到∠1的位置,把∠B移到∠2的位置,从而完成证明的。请你借助图2作辅助线的思路将下面证明“三角形的内角和等于180°”的过程补充完整。
已知:△ABC
求证:∠BAC+∠B+∠C=180°
证明:如图2,过点A作直线DE∥BC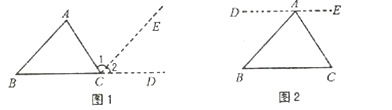
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(a2)3的结果是
A. a5 B. a6 C. a8 D. 3a2
相关试题

