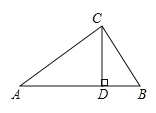
【题目】如图,∠ABD=90°,
(1)点B在直线 上,点D在直线 外;
(2)直线 与直线 相交于点A,点D是直线 与直线 的交点,也是直线 与直线 的交点,又是直线 与直线 的交点;
(3)直线 ⊥直线 ,垂足为点 ;
(4)过点D有且只有 条直线与直线AC垂直.
参考答案:
【答案】AB(或BD),AC;AD,AB,AD,BD,AD,CD,BD,CD;BD,AB,B;一.
【解析】
(1)根据点与直线的位置关系解答即可;
(2)根据相交线的定义解答;
(3)根据垂线的定义解答;
(4)根据垂线的性质进行解答.
(1)由图可知,点B在直线AB(或BD)上,点D在直线AC外.
(2)∵点D是直线AD,BD,CD的交点,
∴直线AD与直线AB相交于点A,点D是直线AD与直线BD的交点,也是直线AD与直线CD的交点,又是直线BD与直线CD的交点.
(3)∵∠ABD=90°,
∴直线BD⊥直线AB,垂足为点B.
(4)∵DB⊥AC,
∴过点D有且只有一条直线与直线AC垂直.
故答案为:AB(或BD),AC;AD,AB,AD,BD,AD,CD,BD,CD;BD,AB,B;一.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业生成一种节能产品,投放市场供不应求.若该企业每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于120万元.已知这种产品的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=190﹣2x.月产量x(套)与生成总成本y2(万元)存在如图所示的函数关系.
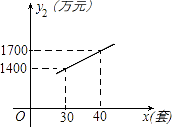
(1)直接写出y2(2)与x之间的函数关系式;
(2)求月产量x的取值范围;
(3)当月产量x(套)为多少时,这种产品的利润W(万元)最大?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】若一次函数
 的图像经过点A(-1,1),下列各点中在该函数图象上的是( )
的图像经过点A(-1,1),下列各点中在该函数图象上的是( )A. (1,5) B. (2,5) C. (-2,-2) D. (0,1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班共有52名同学,在校广播操比赛中排成方队,先把每位同学都进行编号,然后把各自的位置固定下来,如图,在平面直角坐标系中,每个自然数都对应着一个坐标.例如1的对应点是原点
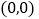 ,3的对应点是
,3的对应点是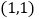 ,16的对应点是
,16的对应点是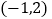 .那么最后一名同学的位置对应的坐标是____,全校学生如果排成这样一个大方阵,编号是2015的学生的对应点的坐标是___.
.那么最后一名同学的位置对应的坐标是____,全校学生如果排成这样一个大方阵,编号是2015的学生的对应点的坐标是___.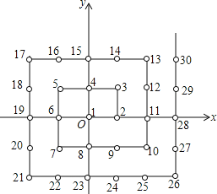
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
 .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为 ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+ ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+ .其中正确结论的序号是 .
.其中正确结论的序号是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=ABAD.我们称该四边形为“可分四边形”,∠DAB称为“可分角”.

(1)如图2,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(2)如图3,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则求∠DAB的度数;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,则△DAB的最大面积等于 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
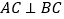 于点C,AC=4,BC=
于点C,AC=4,BC=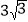 ,将线段AC绕点A按逆时针方向旋转
,将线段AC绕点A按逆时针方向旋转 ,得到线段AD,连接DC,DB,则线段DB的长为__________。
,得到线段AD,连接DC,DB,则线段DB的长为__________。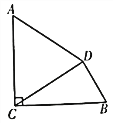
相关试题

