【题目】如图,四边形ABCD为平行四边形纸片.把纸片ABCD折叠,使点B恰好落在CD边上,折痕为AF.且AB=10cm、AD=8cm、DE=6cm.
(1)求证:平行四边形ABCD是矩形;
(2)求BF的长;
(3)求折痕AF长.

参考答案:
【答案】(1)见解析;(2)5cm;(3)5![]() cm.
cm.
【解析】分析:(1)根据翻折变换的对称性可知AE=AB,在△ADE中,利用勾股定理逆定理证明三角形为直角三角形,再根据有一个角是直角的平行四边形是矩形证明即可;
(2)设BF为x,分别表示出EF、EC、FC,然后在△EFC中利用勾股定理列式进行计算即可;
(3)在Rt△ABF中,利用勾股定理求解即可.
详解:(1)证明:∵把纸片ABCD折叠,使点B恰好落在CD边上,
∴AE=AB=10,AE2=102=100,
又∵AD2+DE2=82+62=100,
∴AD2+DE2=AE2,
∴△ADE是直角三角形,且∠D=90°,
又∵四边形ABCD为平行四边形,
∴平行四边形ABCD是矩形(有一个角是直角的平行四边形是矩形);
(2)设BF=x,则EF=BF=x,EC=CD-DE=10-6=4cm,FC=BC-BF=8-x,
在Rt△EFC中,EC2+FC2=EF2,
即42+(8-x)2=x2,
解得x=5,
故BF=5cm;
(3)在Rt△ABF中,由勾股定理得,AB2+BF2=AF2,
∵AB=10cm,BF=5cm,
∴AF=![]() =5
=5![]() cm.
cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“三等分任意角”是数学史上一个著名问题,经过无数人探索,现在已经确信,仅用圆规直尺是不可能做出的.在探索过程中,我们发现,可以利用一些特殊的图形,把一个任意角三等分.如图:在∠MAN的边上任取一点B,过点B作BC⊥AN于点C,并作BC的垂线BF,连接AF,E是AF上一点,当AB=BE=EF时,有∠FAN=
 ∠MAN,请你证明.
∠MAN,请你证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论是________.(写出正确命题的序号)
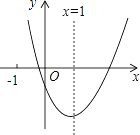
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着我国经济的发展,高铁逐渐成为了主要的交通工具,一般的高铁G字头的高速动车组以D字头的动车组,由大连到北京的G377的平均速度是D31的平均速度的
 倍,行驶相同的路程
倍,行驶相同的路程 千米,G377少用
千米,G377少用 个小时。
个小时。(1)求D31的平均速度。
(2)若以“速度与票价的比值”定义这两种列车的性价比,人们出行都喜欢选择性价比高的方式,现阶段D31票价为
 元/张,G377票件为
元/张,G377票件为 元/张,如果你又机会给有关部门提一个合理化建议,使G377得性价比达到D31的性价比,你如何建议,为什么?
元/张,如果你又机会给有关部门提一个合理化建议,使G377得性价比达到D31的性价比,你如何建议,为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个多项式A=9xy+7xy-x-2,B=3xy-5xy+x+7
(1)求A-3B;
(2)若要使A-3B的值与x的取值无关,试求y的值;
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知|x1-1|+|x2-2|+|x3-3|+…+|x2018-2018|+|x2019-2019|=0,求代数式
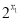 -
-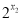 -…-
-…-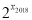 +
+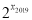 的值.
的值. -
科目: 来源: 题型:
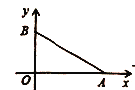
查看答案和解析>>【题目】如图,在平面直角坐标系中,点
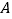 、
、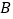 分别在
分别在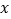 、
、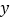 轴上,已知点
轴上,已知点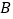 的坐标为
的坐标为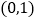 ,且
,且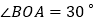 .
.
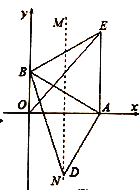
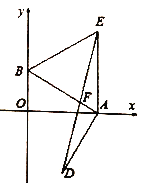
(1) (2) (3)
(1)求
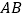 的长度;
的长度;(2)以
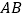 为一边作等边,过点
为一边作等边,过点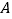 作
作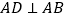 ,交
,交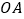 的垂直平分线
的垂直平分线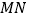 于点
于点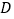 .求证:
.求证: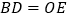 ;
;(3)在(2)的条件下,连接
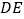 交
交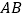 于
于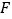 ,求证:
,求证: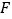 为
为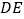 的中点.
的中点.
相关试题

