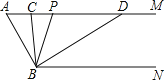
【题目】如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
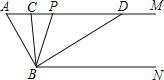
(1)求∠CBD的度数;
(2)当点P运动时,∠APB:∠ADB的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到某处时,∠ACB=∠ABD,求此时∠ABC的度数.
参考答案:
【答案】(1)60°;(2)不变,2:1,见解析;(3)30°
【解析】
(1)根据角平分线的定义只要证明∠CBD=![]() ∠ABN即可;
∠ABN即可;
(2)不变.可以证明∠APB=∠PBN,∠ADB=∠DBN=∠PBN;
(3)想办法证明∠ABC=∠CBP=∠DBP=∠DBN即可解决问题;
(1)∵AM∥BN,
∴∠ABN=180°-∠A=120°,
又∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBD=∠CBP+∠DBP=![]() (∠ABP+∠PBN)=
(∠ABP+∠PBN)=![]() ∠ABN=60°.
∠ABN=60°.
(2)不变.理由如下:
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
又∵BD平分∠PBN,
∴∠ADB=∠DBN=![]() ∠PBN=
∠PBN=![]() ∠APB,即∠APB:∠ADB=2:1.
∠APB,即∠APB:∠ADB=2:1.
(3)∵AM∥BN,
∴∠ACB=∠CBN,
又∵∠ACB=∠ABD,
∴∠CBN=∠ABD,
∴∠ABC=∠ABD-∠CBD=∠CBN-∠CBD=∠DBN,
∴∠ABC=∠CBP=∠DBP=∠DBN,
∴∠ABC=![]() ∠ABN=30°.
∠ABN=30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D,E分别在线段AB,AC上,CD与BE相交于点O,已知AB=AC,那么添加下列一个条件后,仍无法判定
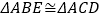 的是( )
的是( )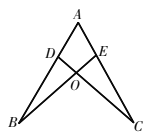
A.
 B. AD=AE C. BE=CD D. BD=CE
B. AD=AE C. BE=CD D. BD=CE -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是由一些棱长都为1的小正方体组合成的简单几何体.

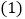 该几何体的表面积
该几何体的表面积 含下底面
含下底面 为______;
为______; 请画出这个几何体的三视图并用阴影表示出来;
请画出这个几何体的三视图并用阴影表示出来; 如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和俯视图不变,那么最多可以再添加______个小正方体.
如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和俯视图不变,那么最多可以再添加______个小正方体. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
, ,说明
,说明 的理由.
的理由.解:因为
 (已知)
(已知)所以
 (____________)
(____________)所以
 (____________)
(____________)因为
 (已知)
(已知)所以
 (等式性质)
(等式性质)即

所以
 (____________)
(____________)所以
 (____________)
(____________)
-
科目: 来源: 题型:
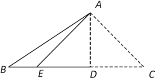
查看答案和解析>>【题目】如图,将三角形纸片ABC沿AD折叠,使点C落在BD边上的点E处.若BC=10,BE=2,则AB2-AC2的值为 ______.
-
科目: 来源: 题型:
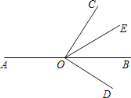
查看答案和解析>>【题目】如图,O是直线AB上一点,
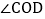 是直角,OE平分
是直角,OE平分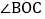 .
.
 若
若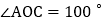 ,则
,则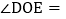 ______;若
______;若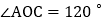 ,则
,则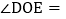 ______;
______;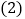 若
若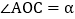 ,则
,则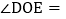 ______
______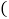 用含
用含 的式子表示
的式子表示 ,请说明理由;
,请说明理由;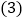 在
在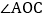 的内部有一条射线OF,满足
的内部有一条射线OF,满足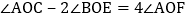 ,试确定
,试确定 与
与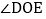 的度数之间的关系,并说明理由.
的度数之间的关系,并说明理由. -
科目: 来源: 题型:
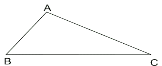
查看答案和解析>>【题目】按要求完成画图和填空:
(1)作
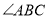 的角平分线
的角平分线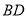 ;
;(2)作出边
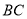 的中垂线
的中垂线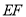 ,垂足为
,垂足为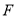 ,交
,交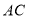 于点
于点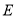 ;
;(3)过点
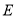 作边
作边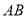 的平行线,交
的平行线,交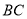 于点
于点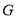 ;
;(4)点
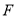 到边
到边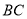 的距离是_____________.
的距离是_____________.(要求:尺规作图,保留作图痕迹,不写作法,写出结论)
相关试题

