【题目】如图,△ABC中,∠ACB=72°,将△ABC绕点B按逆时针方向旋转得到△BDE(点D与点 A是对应点,点E与点C是对应点),且边DE恰好经过点C,则∠ABD的度数为

A. 36° B. 40° C. 45° D. 50°
参考答案:
【答案】A
【解析】先根据旋转的性质可知BE=BC,∠BED=∠ACB=72°,∠ABC=∠EBD,再根据等腰三角形的性质和三角形内角和的性质可求得∠EBC= 36°,从而得出∠ABD=36°.
∵△ABC绕点B按逆时针方向旋转得到△BDE(点D与点 A是对应点,点E与点C是对应点),
∴BE=BC,∠BED=∠ACB=72°∠ABC=∠EBD.
∴∠ABC-∠DBC =∠EBD-∠DBC.
即:∠ABD=∠EBC。
∵BE=BC,
∴∠BCE=∠BEC=72°.
在△BCE中,∠BCE+∠BEC+∠CBE=180°,
∴∠CBE=36°,
∴∠ABD=∠EBC=36°.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上,点
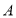 表示1,现将点
表示1,现将点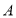 沿
沿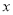 轴做如下移动,第一次点
轴做如下移动,第一次点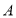 向左移动3个单位长度到达点
向左移动3个单位长度到达点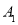 ,第二次将点
,第二次将点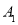 向右移动6个单位长度到达点
向右移动6个单位长度到达点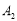 ,第三次将点
,第三次将点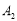 向左移动9个单位长度到达点
向左移动9个单位长度到达点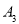 ,按照这种移动规律移动下去,第
,按照这种移动规律移动下去,第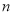 次移动到点
次移动到点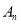 ,如果点
,如果点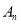 与原点的距离不小于20,那么
与原点的距离不小于20,那么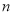 的最小值是__________.
的最小值是__________.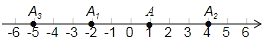
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学在一次用频率去估计概率的实验中,统一了某一结果出现的频率绘出的统计图 如图所示,则符合这一结果的实验可能是( )
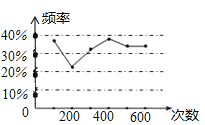
A.从一个装有2个白球和1个红球的袋子中任取两球,取到两个白球的概率
B.任意写一个正整数,它能被 2 整除的概率
C.抛一枚硬币,连续两次出现正面的概率
D.掷一枚正六面体的骰子,出现 1 点的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图有一张简易的活动小餐桌,现测得OA=OB=30cm,OC=OD=50cm,桌面离地面的高度为40cm,则两条桌腿的张角∠COD的度数为______度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】探究:
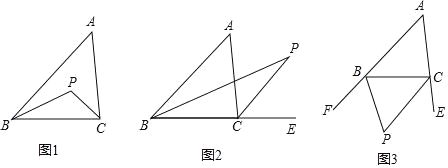
(1)如图1,在△ABC中,BP平分∠ABC,CP平分∠ACB.求证:∠P=90°+
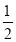 ∠A.
∠A.(2)如图2,在△ABC中,BP平分∠ABC,CP平分外角∠ACE.猜想∠P和∠A有何数量关系,并证明你的结论.
(3)如图3,BP平分∠CBF,CP平分∠BCE.猜想∠P和∠A有何数量关系,请直接写出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一些半径相同的小圆按如图所示的规律摆放:
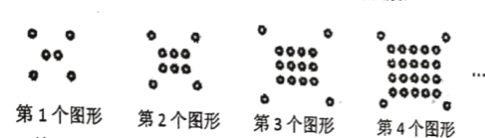
(1)填写下表:
图形序号
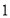
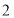
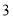
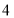
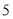
小圆个数
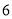
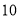
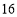
(2)照这样的规律搭下去,摆
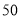 个这样的图形需要 个小圆.
个这样的图形需要 个小圆. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知直线PQ∥MN,点A在直线PQ上,点C、D在直线MN上,连接AC、AD,∠PAC=50°,∠ADC=30°,AE平分∠PAD,CE平分∠ACD,AE与CE相交于E.
(1)求∠AEC的度数;
(2)若将图1中的线段AD沿MN向右平移到A1D1如图2所示位置,此时A1E平分∠AA1D1,CE平分∠ACD1,A1E与CE相交于E,∠PAC=50°,∠A1D1C=30°,求∠A1EC的度数.
(3)若将图1中的线段AD沿MN向左平移到A1D1如图3所示位置,其他条件与(2)相同,求此时∠A1EC的度数.

相关试题

