【题目】阅读材料:
①直线l外一点P到直线l的垂线段的长度,叫做点P到直线l的距离,记作d(P,l);
②两条平行线![]() ,
,![]() ,直线
,直线![]() 上任意一点到直线
上任意一点到直线![]() 的距离,叫做这两条平行线
的距离,叫做这两条平行线![]() ,
,![]() 之间的距离,记作d(
之间的距离,记作d(![]() ,
,![]() );
);
③若直线![]() ,
,![]() 相交,则定义d(
相交,则定义d(![]() ,
,![]() )=0;
)=0;
④若直线![]() ,
,![]() 重合,我们定义d(
重合,我们定义d(![]() ,
,![]() )=0,
)=0,
对于两点![]() ,
,![]() 和两条直线
和两条直线![]() ,
,![]() ,定义两点
,定义两点![]() ,
,![]() 的“
的“![]() ,
,![]() 相关距离”如下:
相关距离”如下:
d(![]() ,
,![]() |
|![]() ,
,![]() )=d(
)=d(![]() ,
,![]() )+d(
)+d(![]() ,
,![]() )+d(
)+d(![]() ,
,![]() )
)
设![]() (4,0),
(4,0),![]() (0,3),
(0,3),![]() :y=x,
:y=x,![]() :y=
:y=![]() ,
,![]() :y=kx,解决以下问题:
:y=kx,解决以下问题:
(1)d(![]() ,
,![]() |
|![]() ,
,![]() )= ;
)= ;
(2)①若k>0,则当d(![]() ,
,![]() |
|![]() ,
,![]() )最大时,k= ;
)最大时,k= ;
②若k<0,试确定k的值,使得d(![]() ,
,![]() |
|![]() ,
,![]() )最大,请说明理由.
)最大,请说明理由.

参考答案:
【答案】(1) ![]() ;(2)①
;(2)①![]() ;②
;②![]() .
.
【解析】
试题分析:(1)首先分别求出d(![]() ,
,![]() )、d(
)、d(![]() ,
,![]() )、d(
)、d(![]() ,
,![]() )的值各是多少,再把它们求和,求出d(
)的值各是多少,再把它们求和,求出d(![]() ,
,![]() |
|![]() ,
,![]() )的值是多少;然后分别求出d(
)的值是多少;然后分别求出d(![]() ,
,![]() )、d(
)、d(![]() ,
,![]() )、d(
)、d(![]() ,
,![]() )的值各是多少,再把它们求和,求出d(
)的值各是多少,再把它们求和,求出d(![]() ,
,![]() |
|![]() ,
,![]() )的值是多少即可.
)的值是多少即可.
(2)①首先作![]() A⊥
A⊥![]() 于点A,
于点A,![]() B⊥
B⊥![]() 于点B,连接
于点B,连接![]()
![]() 交
交![]() 于点C,然后根据
于点C,然后根据![]() A+
A+![]() B≤
B≤![]()
![]() ,可得当
,可得当![]()
![]() ⊥
⊥![]() 时,
时,![]() A+
A+![]() B的值最大,据此求出k的值是多少即可.
B的值最大,据此求出k的值是多少即可.
②首先作![]() A⊥
A⊥![]() 于点A,
于点A,![]() B⊥
B⊥![]() 于点B,
于点B,![]() 、
、![]() 关于原点对称,
关于原点对称,![]() C⊥
C⊥![]() 于点C,
于点C,![]()
![]() 交
交![]() 于点D,然后根据
于点D,然后根据![]() B+
B+![]() C≤
C≤![]()
![]() ,可得当
,可得当![]()
![]() ⊥
⊥![]() 时,
时,![]() B+
B+![]() C取到最大值,据此求出k的值是多少即可.
C取到最大值,据此求出k的值是多少即可.
试题解析:(1)∵![]() (4,0),
(4,0),![]() (0,3),
(0,3),![]() :y=x,
:y=x,![]() :y=
:y=![]() ,
,
∴d(![]() ,
,![]() |
|![]() ,
,![]() )=d(
)=d(![]() ,
,![]() )+d(
)+d(![]() ,
,![]() )+d(
)+d(![]() ,
,![]() )=
)=![]() =
=![]() ;
;
∴d(![]() ,
,![]() |
|![]() ,
,![]() )= d(
)= d(![]() ,
,![]() )+d(
)+d(![]() ,
,![]() )+d(
)+d(![]() ,
,![]() )=
)=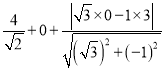 =
=![]() .
.
故答案为:![]() ;
;
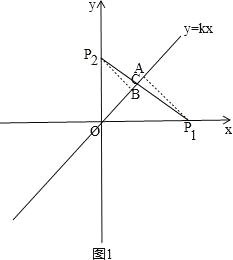
(2)①如图1,作![]() A⊥
A⊥![]() 于点A,
于点A,![]() B⊥
B⊥![]() 于点B,连接
于点B,连接![]()
![]() 交
交![]() 于点C,
于点C,
d(![]() ,
,![]() |
|![]() ,
,![]() )=d(
)=d(![]() ,
,![]() )+d(
)+d(![]() ,
,![]() )+d(
)+d(![]() ,
,![]() )=
)=![]() A+
A+![]() B,
B,
∵![]() A≤
A≤![]() C,
C,![]() B≤
B≤![]() C,
C,
∴![]() A+
A+![]() B≤
B≤![]()
![]() ,
,
∴当![]()
![]() ⊥
⊥![]() 时,
时,
![]() A+
A+![]() B的最大值是:
B的最大值是:![]() =5,
=5,
此时k=tan∠O![]()
![]() =
=![]() =
=![]() ,
,
∴若k>0,当d(![]() ,
,![]() |
|![]() ,
,![]() )最大时,k=
)最大时,k=![]() .
.
故答案为:![]() ;
;
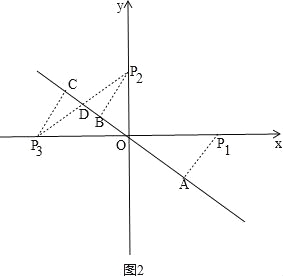
②如图2,作![]() A⊥
A⊥![]() 于点A,
于点A,![]() B⊥
B⊥![]() 于点B,
于点B,![]() 、
、![]() 关于原点对称,
关于原点对称,![]() C⊥
C⊥![]() 于点C,
于点C,![]()
![]() 交
交![]() 于点D,
于点D,
∵![]() 、
、![]() 关于原点对称,
关于原点对称,
∴![]() A=
A=![]() C,
C,
∴d(![]() ,
,![]() |
|![]() ,
,![]() )=d(
)=d(![]() ,
,![]() )+d(
)+d(![]() ,
,![]() )+d(
)+d(![]() ,
,![]() )=
)=![]() A+
A+![]() B=
B=![]() B+
B+![]() C,
C,
∵![]() B≤
B≤![]() D,
D,![]() C≤
C≤![]() D,
D,
∴![]() B+
B+![]() C≤
C≤![]()
![]() ,
,
∴当![]()
![]() ⊥
⊥![]() 时,
时,
![]() B+
B+![]() C的最大值是:
C的最大值是:![]() =
=![]() =5,
=5,
此时k=﹣tan∠O![]()
![]() =
=![]() =
=![]() ,
,
∴若k<0,当d(![]() ,
,![]() |
|![]() ,
,![]() )最大时,k=
)最大时,k=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为( )
A.42 B.32 C.42 或 32 D.37 或 33
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列条件,只能画出唯一的△ABC的是( )
A. AB=3 BC=4 B. AB=4 BC=3 ∠A=30°
C. ∠A=60°∠B=45° AB=4 D. ∠C=60°AB=5
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)数学爱好者小森偶然阅读到这样一道竞赛题:
一个圆内接六边形ABCDEF,各边长度依次为 3,3,3,5,5,5,求六边形ABCDEF的面积.
小森利用“同圆中相等的弦所对的圆心角相等”这一数学原理,将六边形进行分割重组,得到图③.可以求出六边形ABCDEF的面积等于 .

(2)类比探究:一个圆内接八边形,各边长度依次为2,2,2,2,3,3,3,3.求这个八边形的面积.请你仿照小森的思考方式,求出这个八边形的面积.
-
科目: 来源: 题型:
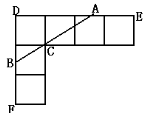
查看答案和解析>>【题目】已知:正方形的边长为1.(1)如图(a),可以计算出正方形的对角线长为
 .如图(b),求两个并排成的矩形的对角线的长.n个呢?(2)若把(c)(d)两图拼成如下“L”形,过C作直线交DE于A,交DF于B.若DB=
.如图(b),求两个并排成的矩形的对角线的长.n个呢?(2)若把(c)(d)两图拼成如下“L”形,过C作直线交DE于A,交DF于B.若DB=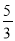 ,求DA的长度.
,求DA的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣17+(﹣33)﹣10﹣(﹣16).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠长方形一边AD,点D落在BC边的点F处,BC=10cm,AB=8cm。

求:(1)FC的长;
(2)EF的长。
相关试题

