【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
①四边形CFHE是菱形;
②EC平分∠DCH;
③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2 ![]() .
.
以上结论中,你认为正确的有 . (填序号)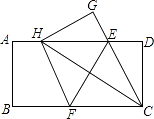
参考答案:
【答案】①③④
【解析】解:∵FH与CG,EH与CF都是矩形ABCD的对边AD、BC的一部分,
∴FH∥CG,EH∥CF,
∴四边形CFHE是平行四边形,
由翻折的性质得,CF=FH,
∴四边形CFHE是菱形,(故①正确);
∴∠BCH=∠ECH,
∴只有∠DCE=30°时EC平分∠DCH,(故②错误);
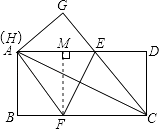
点H与点A重合时,设BF=x,则AF=FC=8﹣x,
在Rt△ABF中,AB2+BF2=AF2,
即42+x2=(8﹣x)2,
解得x=3,
点G与点D重合时,CF=CD=4,
∴BF=4,
∴线段BF的取值范围为3≤BF≤4,(故③正确);
过点F作FM⊥AD于M,
则ME=(8﹣3)﹣3=2,
由勾股定理得,
EF= ![]() =
= ![]() =2
=2 ![]() ,(故④正确);
,(故④正确);
综上所述,结论正确的有①③④共3个,
故答案为①③④.
①先判断出四边形CFHE是平行四边形,再根据翻折的性质可得CF=FH,然后根据邻边相等的平行四边形是菱形证明,判断出①正确;
②根据菱形的对角线平分一组对角线可得∠BCH=∠ECH,然后求出只有∠DCE=30°时EC平分∠DCH,判断出②错误;
③点H与点A重合时,设BF=x,表示出AF=FC=8-x,利用勾股定理列出方程求解得到BF的最小值,点G与点D重合时,CF=CD,求出BF=4,然后写出BF的取值范围,判断出③正确;
④过点F作FM⊥AD于M,求出ME,再利用勾股定理列式求解得到EF,判断出④正确。
-
科目: 来源: 题型:
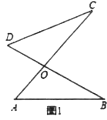
查看答案和解析>>【题目】小学我们已经知道三角形三个内角和是180°,对于如图1中,
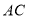 ,
,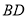 交于
交于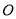 点,形成的两个三角形中的角存在以下关系:①
点,形成的两个三角形中的角存在以下关系:①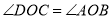 ;②
;②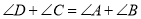 .试探究下面问题:
.试探究下面问题:已知
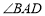 的平分线
的平分线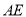 与
与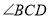 的平分线
的平分线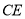 交于点
交于点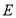 ,
,
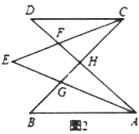
(1)如图2,若
 ,
,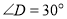 ,
,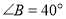 ,则
,则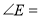 _________;
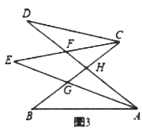
_________;(2)如图3,若
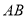 不平行
不平行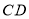 ,
,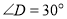 ,
,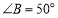 ,则
,则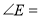 _______.
_______.(3)在总结前两问的基础上,借助图3,探究
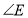 与
与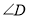 、
、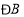 之间是否存在某种等量关系?若存在,请说明理由;若不存在,请举例说明.
之间是否存在某种等量关系?若存在,请说明理由;若不存在,请举例说明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸上的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形.在建立平面直角坐标系后,点B的坐标为(﹣2,﹣1).
(1)把△ABC向左平移4格后得到△A1B1C1,画出△A1B 1C1并写出点A1的坐标;
(2)把△ABC绕点C按顺时针旋转90°后得到△A2B2C,画出△A2B2C的图形并写出点A2的坐标.

-
科目: 来源: 题型:
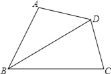
查看答案和解析>>【题目】如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,
求证:∠A+∠C=180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,∠B=∠CAD.

(1)求证:AC是⊙O的切线;
(2)若点E是 的中点,连接AE交BC于点F,当BD=5,CD=4时,求AF的值.
的中点,连接AE交BC于点F,当BD=5,CD=4时,求AF的值. -
科目: 来源: 题型:
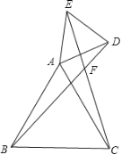
查看答案和解析>>【题目】如图,已知△ABC和△ADE均为等边三角形,BD、CE交于点F.
(1)求证:BD=CE;(2)求锐角∠BFC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学八年级的篮球队有10名队员
 在“二分球”罚篮投球训练中,这10名员各投篮50次的进球情况如下表:
在“二分球”罚篮投球训练中,这10名员各投篮50次的进球情况如下表:进球数
42
32
26
20
19
18
人数
1
1
2
1
2
3
针对这次训练,请解答下列问题:
 求这10名队员进球数的平均数、中位数;
求这10名队员进球数的平均数、中位数; 求这支球队投篮命中率______;
求这支球队投篮命中率______; 若队员小亮“二分球”的投篮命中率为
若队员小亮“二分球”的投篮命中率为 ,请你分析一下小亮在这支球队中的投篮水平.
,请你分析一下小亮在这支球队中的投篮水平. 投篮命中率
投篮命中率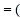 进球数
进球数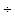 投篮次数
投篮次数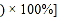
相关试题

