【题目】如图,AB是⊙O的直径,∠B=∠CAD. 
(1)求证:AC是⊙O的切线;
(2)若点E是 ![]() 的中点,连接AE交BC于点F,当BD=5,CD=4时,求AF的值.
的中点,连接AE交BC于点F,当BD=5,CD=4时,求AF的值.
参考答案:
【答案】
(1)证明:∵AB是⊙O的直径,
∴∠ADB=∠ADC=90°,
∵∠B=∠CAD,∠C=∠C,
∴△ADC∽△BAC,
∴∠BAC=∠ADC=90°,
∴BA⊥AC,
∴AC是⊙O的切线
(2)解:∵BD=5,CD=4,
∴BC=9,
∵△ADC∽△BAC(已证),
∴ ![]() =
= ![]() ,即AC2=BC×CD=36,
,即AC2=BC×CD=36,
解得:AC=6,
在Rt△ACD中,AD= ![]() =2
=2 ![]() ,
,
∵∠CAF=∠CAD+∠DAE=∠ABF+∠BAE=∠AFD,
∴CA=CF=6,
∴DF=CA﹣CD=2,
在Rt△AFD中,AF= ![]() =2
=2 ![]()
【解析】(1)证明△ADC∽△BAC,可得∠BAC=∠ADC=90°,继而可判断AC是⊙O的切线.(2)根据(1)所得△ADC∽△BAC,可得出CA的长度,继而判断∠CFA=∠CAF,利用等腰三角形的性质得出AF的长度,继而得出DF的长,在Rt△AFD中利用勾股定理可得出AF的长.
【考点精析】解答此题的关键在于理解切线的判定定理的相关知识,掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸上的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形.在建立平面直角坐标系后,点B的坐标为(﹣2,﹣1).
(1)把△ABC向左平移4格后得到△A1B1C1,画出△A1B 1C1并写出点A1的坐标;
(2)把△ABC绕点C按顺时针旋转90°后得到△A2B2C,画出△A2B2C的图形并写出点A2的坐标.

-
科目: 来源: 题型:
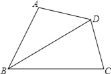
查看答案和解析>>【题目】如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,
求证:∠A+∠C=180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
①四边形CFHE是菱形;
②EC平分∠DCH;
③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2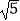 .
.
以上结论中,你认为正确的有 . (填序号)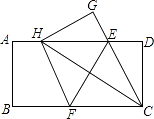
-
科目: 来源: 题型:
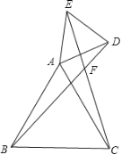
查看答案和解析>>【题目】如图,已知△ABC和△ADE均为等边三角形,BD、CE交于点F.
(1)求证:BD=CE;(2)求锐角∠BFC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学八年级的篮球队有10名队员
 在“二分球”罚篮投球训练中,这10名员各投篮50次的进球情况如下表:
在“二分球”罚篮投球训练中,这10名员各投篮50次的进球情况如下表:进球数
42
32
26
20
19
18
人数
1
1
2
1
2
3
针对这次训练,请解答下列问题:
 求这10名队员进球数的平均数、中位数;
求这10名队员进球数的平均数、中位数; 求这支球队投篮命中率______;
求这支球队投篮命中率______; 若队员小亮“二分球”的投篮命中率为
若队员小亮“二分球”的投篮命中率为 ,请你分析一下小亮在这支球队中的投篮水平.
,请你分析一下小亮在这支球队中的投篮水平. 投篮命中率
投篮命中率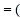 进球数
进球数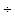 投篮次数
投篮次数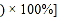
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明一家利用国庆八天驾车到某景点旅游,小汽车出发前油箱有油35L,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图像回答下列问题:
(1)小汽车行驶______h后加油,中途加油_______L
(2)求加油前油箱余油量Q与行驶时间t的函数关系式
(3)如果小汽车在行驶过程中耗油量速度不变,加油站距景点200km,车速80km/h,要到达目的地,油箱中的油是否够用?请说明理由

相关试题

