【题目】如图,大楼![]() (可以看作不透明的长方体)的四周都是空旷的水平地面.地面上有甲、乙两人,他们现在分别位于点
(可以看作不透明的长方体)的四周都是空旷的水平地面.地面上有甲、乙两人,他们现在分别位于点![]() 和点
和点![]() 处,
处,![]() 、
、![]() 均在
均在![]() 的中垂线上,且
的中垂线上,且![]() 、
、![]() 到大楼的距离分别为
到大楼的距离分别为![]() 米和
米和![]() 米,又已知
米,又已知![]() 长
长![]() 米,
米,![]() 长
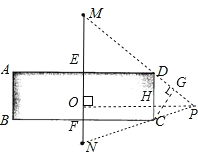
长![]() 米,由于大楼遮挡着,所以乙不能看到甲.若乙沿着大楼的外面地带行走,直到看到甲(甲保持不动),则他行走的最短距离长为________米.
米,由于大楼遮挡着,所以乙不能看到甲.若乙沿着大楼的外面地带行走,直到看到甲(甲保持不动),则他行走的最短距离长为________米.

参考答案:
【答案】![]()
【解析】
据已知首先得出DH=HP=x米,NO=(20![]() +40-x)米,PO=(60+x)米,再利用平行线分线段成比例定理和三角形面积求出即可.
+40-x)米,PO=(60+x)米,再利用平行线分线段成比例定理和三角形面积求出即可.
连接MD并延长,连接NC并延长,使其两延长线相交于点P,
作PO⊥MN于O,作CG⊥MP于G,
根据题意可得出:
ME=60,DE=HO=FC=60米,FN=20![]() 米,EF=40,
米,EF=40,
∴NC=![]() ,
,
=40![]() 米,
米,
设EO=x米,
∴DH=x米,
∵ME=DE=60米,
∴∠MDE=45,
∴DH=HP=x米,NO=(20![]() +40x)米,PO=(60+x)米,
+40x)米,PO=(60+x)米,
∵FC∥PO,
∴![]() ,
,
∴x![]() ,
,
解得:x=6020![]() ,
,
∴PO=(12020![]() )米,NO=(40
)米,NO=(40![]() 20)米,
20)米,
![]() CDHP=
CDHP=![]() DPCG,
DPCG,
![]() ×40×(12020
×40×(12020![]() 60)=
60)= ![]() ×
×![]() [20
[20![]() +40(40
+40(40![]() 20)]CG,
20)]CG,
CG=20![]() 米,
米,
∴行走的最短距离长为:NC+CG=(40![]() +20
+20![]() )米.
)米.
故答案为:40![]() +20
+20![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以点P(-1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=
 ,将△ABC绕点P旋转180°,得到△MCB.
,将△ABC绕点P旋转180°,得到△MCB. 
(1)求B、C两点的坐标;
(2)请在图中画出线段MB、MC,并判断四边形ACMB的形状(不必证明),求出点M的坐标;
(3)动直线l从与BM重合的位置开始绕点B顺时针旋转,到与BC重合时停止,设直线l与CM交点为E,点Q为BE的中点,过点E作EG⊥BC于G,连接MQ、QG.请问在旋转过程中∠MQG的大小是否变化?若不变,求出∠MQG的度数;若变化,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,梯子AB靠在墙上,梯子的底端A到墙根O的距离为2m,梯子顶端B到地面距离为7m,现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离等于4m,同时梯子的顶端B下降至B′,那么BB′的长为( )

A. 等于1mB. 大于1mC. 小于1mD. 以上答案都不对
-
科目: 来源: 题型:
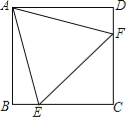
查看答案和解析>>【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=
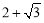 .
.其中正确的序号是 (把你认为正确的都填上).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了推动我县“三进校园”活动的广泛开展,引导学生走向操场,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据相关信息,解答下列问题:

(1)本次接受随机抽样调查的学生人数为 ,图①中
 的值为 ;
的值为 ;(2)本次调查获取的样本数据的众数为 ,中位数为 ;
(3)根据样本数据,若学校计划购买
 双运动鞋,建议购买
双运动鞋,建议购买 号运动鞋 双.
号运动鞋 双. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强公民的节水意识,合理利用水资源,各地采用价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过6立方米时,水费按每立方米a元收费,超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按c元收费,该市某户今年9、10月份的用水量和所交水费如下表所示:

设某户每月用水量x(立方米),应交水费y(元)
(1)a= ,c=
(2)当x≤6,x≥6时,分别求出y于x的函数关系式
(3)若该户11月份用水量为8立方米,求该户11 月份水费是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC和△DEF,点E在BC边上,点A在DE边上,边EF和边AC相交于点G.如果AE=EC,∠AEG=∠B,那么添加下列一个条件后,仍无法判定△DEF与△ABC一定相似的是( )

A.
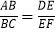 B.
B. 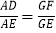 C.
C.  D.
D. 
相关试题

