【题目】如图,已知△ABC中,BD、CE是高, F是BC中点,连接DE、EF和DF,
(1)求证:△DEF是等腰三角形.
(2)若∠A=45°,试判断△DEF的形状,并说明理由. (3)若∠A:∠DFE=5:2,BC=4,求△DEF的面积.

参考答案:
【答案】(1)证明见试题解析;(2)△DEF是等腰直角三角形,理由见试题解析;(3)1.
【解析】试题分析:(1)由直角三角形斜边上直线的性质可得:EF=![]() BC=DF;故△DEF为等腰三角形;
BC=DF;故△DEF为等腰三角形;
(2)由△BEF和△DFC为等腰三角形和∠A=45°,求出∠EFD的度数即可;
(3)设∠A=5![]() ,则∠DFE=2
,则∠DFE=2![]() ,用(2)类似的方法求出∠DFE=30°,作出△EDF边DF上的高EG,求出EG的长即可.
,用(2)类似的方法求出∠DFE=30°,作出△EDF边DF上的高EG,求出EG的长即可.
试题解析:(1)证明:∵BD、CE是高,F是BC中点,∴EF=![]() BC=DF,∴△DEF是等腰三角形.
BC=DF,∴△DEF是等腰三角形.
(2)△DEF是等腰直角三角形;理由:∵∠A=45°,∴∠EBF+∠DCF=180°-45°=135°,∵EF=![]() BC=DF,∴∠EBF=∠FEB,同理,∠DCF=∠FDC,∴∠FEB+∠FDC=135°,
BC=DF,∴∠EBF=∠FEB,同理,∠DCF=∠FDC,∴∠FEB+∠FDC=135°,
∴∠BFE+∠CFD=180°+180°-135°-135°=90°,∴∠DFE=180°-90°=90°,∴△DEF是等腰直角三角形.
(3)作EG⊥DF于G,设∠A=5![]() ,∠DFE=2
,∠DFE=2![]() ,∵EF=BF,DF=FC,∴∠FBE=∠BEF,∠FCD=∠FDC,
,∵EF=BF,DF=FC,∴∠FBE=∠BEF,∠FCD=∠FDC,
∴∠BFE+∠CFD=180°-2∠FBE+180°-2∠FCD=2(180°-∠FBE-∠FCD)=2∠A=![]() ,∵
,∵![]() ,∴∠DFE=2
,∴∠DFE=2![]() ,∵BC=4,∴DF=EF=2,∴EG=1,∴△DEF面积1.
,∵BC=4,∴DF=EF=2,∴EG=1,∴△DEF面积1.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=kx+6经过点(3,0).
(1)求k的值;
(2)点A(-2,a),B(0.5,b)在直线y=kx+6的图象上试比较a,b的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将下列多项式分解因式,结果中不含因式x﹣1的是( )
A. x2﹣1 B. x(x﹣2)+(2﹣x) C. x2﹣2x+1 D. x2+2x+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班为了奖励在学校体育运动会中表现突出的同学,班主任派生活委员小明到文具店为获奖的同学买奖品,小明发现,如果买1本笔记本和3支钢笔,则需要19元;如果买2本笔记本和5支钢笔,则需要33元.
(1)求购买每本笔记本和每支钢笔各多少元?
(2)班主任给小明的班费只有110元,要奖励24名同学每人一件奖品,则小明至少要购买多少本笔记本?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N,
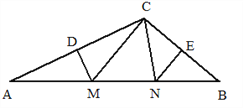
(1)若△CMN的周长为21cm,求AB的长;
(2)若∠MCN=50°,求∠ACB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,被誉为“中原第一高楼”的郑州会展宾馆(俗称“玉米楼”)就坐落在风景如画的如意湖畔,也是来郑观光的游客留影的最佳景点.学完了三角函数后,刘明和王华决定用自己学到的知识测量“玉米楼”的高度.如图2,刘明在点C处测得楼顶B的仰角为45°,王华在高台上测得楼顶的仰角为30°.若高台高DE为5米,点D到点C的水平距离EC为187.5米,A、C、E三点共线,求“玉米楼”AB的高(
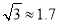 ,结果保留整数).
,结果保留整数).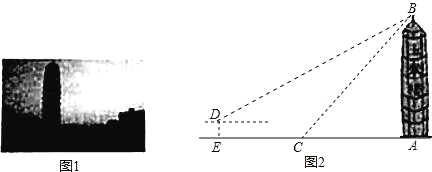
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线AB和抛物线交于点A(-4,0),B(0,4),且点B是抛物线的顶点.
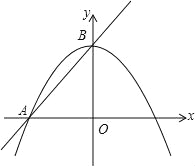
(1)求直线AB和抛物线的解析式.
(2)点P是直线上方抛物线上的一点,求当△PAB面积最大时点P的坐标.
(3)M是直线AB上一动点,在平面直角坐标系内是否存在点N,使以O、B、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.
相关试题

