【题目】如图,六边形ABCDEF与六边形A′B′C′D′E′F′相似.
求:(1)相似比;
(2)∠A和∠B′的度数;
(3)边CD,EF,A′F′,E′D′的长.


参考答案:
【答案】(1)![]() ;(2) ∠A=90°,∠B′=150°;(3)CD=
;(2) ∠A=90°,∠B′=150°;(3)CD=![]() cm,EF=
cm,EF=![]() cm,A′F′=
cm,A′F′=![]() cm,E′D′=
cm,E′D′=![]() cm.
cm.
【解析】(1)对应边的比就是相似比;(2)利用相似多边形对应角相等,可求出结果;(3)利用相似多边形性质列出比例式求解.
解:(1)∵六边形ABCDEF与六边形A′B′C′D′E′F′相似,BC与B′C′是对应边,
∴![]() ,即相似比为
,即相似比为![]() .
.
(2)∵六边形ABCDEF与六边形A′B′C′D′E′F′相似,∴∠A=∠A′,∠B=∠B′.又∵∠A′=90°,∠B=150°,∴∠A=90°,∠B′=150°.
(3)∵六边形ABCDEF与六边形A′B′C′D′E′F′相似,∴![]() =
=![]() =
=![]() =
=![]() =
=![]() .
.
由![]() =
=![]() ,AF=4 cm,得
,AF=4 cm,得![]() =
=![]() ,
,
∴A′F′=![]() (cm).
(cm).
由![]() =
=![]() ,E′F′=4 cm,得
,E′F′=4 cm,得![]() =
=![]() ,
,
∴EF=![]() (cm).
(cm).
由![]() =
=![]() ,ED=5 cm,得
,ED=5 cm,得![]() =
=![]() ,
,
∴E′D′=![]() (cm).
(cm).
由![]() =
=![]() ,C′D′=3 cm,得
,C′D′=3 cm,得![]() =
=![]() ,
,
∴CD=![]() (cm).
(cm).
即CD=![]() cm,EF=
cm,EF=![]() cm,A′F′=
cm,A′F′=![]() cm,E′D′=
cm,E′D′=![]() cm.
cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…若m3分裂后,其中有一个奇数是2017,则m的值是( )
A. 43 B. 44 C. 45 D. 46
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在RtΔABC中,AD是斜边BC上的高,∠B=30°,那么线段BD与CD的数量关系为( )
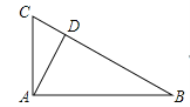
A. BD=CDB. BD=2CDC. BD=3CDD. BD=4CD
-
科目: 来源: 题型:
查看答案和解析>>【题目】将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=
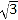 ,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )
,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )
A.
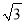 B. 3 C. 2 D. 2
B. 3 C. 2 D. 2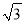
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只蚂蚁从
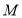 点出发,在一条直线上来回爬行,把它向右爬行的路程记为正数,向左爬行的路程记为负数,则它爬过的各段路程依次为
点出发,在一条直线上来回爬行,把它向右爬行的路程记为正数,向左爬行的路程记为负数,则它爬过的各段路程依次为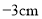 ,
,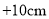 ,
,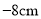 ,
,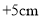 ,
,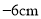 ,
,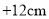 ,
,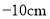 ,
,(1)蚂蚁离出发点最远时是多少厘米?是在出发点的左边还是右边?
(2)蚂蚁在爬行过程中,如果每爬行
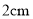 就得到1粒瓜子,那么最后它共得到多少粒瓜子?
就得到1粒瓜子,那么最后它共得到多少粒瓜子? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ΔABC中,∠A=90°,∠C=45°,BC=8,∠ABC的角平分线交AC于点D,DE⊥BC,则CΔDEC=___________。
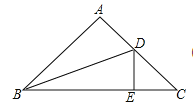
-
科目: 来源: 题型:
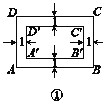
查看答案和解析>>【题目】如图,矩形ABCD的长AB=30,宽BC=20.
(1)如图①,若在矩形ABCD的内部沿四周有宽为1的环形区域,矩形A′B′C′D′与矩形ABCD相似吗?请说明理由;
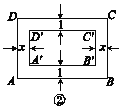
(2)如图②,当x为多少时,矩形ABCD与矩形A′B′C′D′相似?
相关试题

