【题目】为增强公民节水意识,合理利用水资源,某市采用“阶梯收费”,标准如下表:
用水量 | 单价 |
不超过6m3 的部分 | 2元/ m3 |
超过6m3不超过10m3的部分 | 4元/m3 |
超出10m3的部分 | 8元/m3 |
譬如:某用户2月份用水9m3,则应缴水费:2×6+4×(9-6)=24(元)
(1)某用户3月用水15 m3应缴水费多少元?
(2) 已知某用户4月份缴水费20元,求该用户4月份的用水量;
(3) 如果该用户5、6月份共用水20m3 (6月份用水量超过5月份用水量),共交水费64元,则该户居民5、6月份各用水多少立方米?
参考答案:
【答案】(1)应收水费68元.(2)该户4月份用水8m3;(3)5月份用水8m3,6月份用水量为12m3.
【解析】试题分析:(1)不超过6m3,单价为2元,超出超出6m3不超出10m3的部分,单价为4元/m3,超出10m3的部分,单价为8元/m3,根据水费=单价×数量即可求得应收水费;
(2)可以首先求出当用水10m3时的费用为2×6+4×4=28元,根据该户居民4月份交水费20元,即可得出该户4月份用水超过6m3不超过10m3,进而列出方程即可;
(3)应分情况讨论:5月份不超过6m3,6月份10立方米以上;或5月份超过6m3,在6-10立方米之间;以及5月份在10m3以上分别分析即可得出答案.
试题解析:(1)应收水费2×6+4×(10﹣6)+8×(15﹣10)=68元.
(2)∵该用户4月份交水费20元,20<28,
∴设该户居民4月份用水xm3 (x<10),
根据题意得出: 6×2+4×(x﹣6)=20,
解得:x=8;
故该户4月份用水8m3;
(3)①当5月份用水不超过6m3时,设5月份用水xm3,则6月份用水(20﹣x)m3,
根据题意得出:2x+2×6+4×4+8(20﹣x﹣10)=64,
解之得:x=![]() >6,不符合题意舍去.
>6,不符合题意舍去.
②当5月份用水超过6m3时,但不超过10m3时,设5月份用水xm3,
则2×6+4(x﹣6)+2×6+4×4+8×(20﹣10﹣x)=64
解之得:x=8<10符合题意.
③当5月份用水超过10m3时,根据6月份用水量超过5月份用水量,
故不合题意.
所以5月份用水8m3,6月份用水量为12m3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AD=
 AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②AB=HF,③BH=HF;④BC﹣CF=2HE;⑤OE=OD;其中正确结论的序号是_____________
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②AB=HF,③BH=HF;④BC﹣CF=2HE;⑤OE=OD;其中正确结论的序号是_____________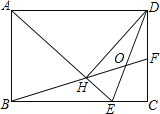
-
科目: 来源: 题型:
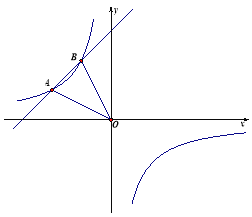
查看答案和解析>>【题目】如图一次函数的图象与反比例函数
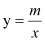 的图象交于A(-4,a)、B两点,点B的横坐标比点A的横坐标大2,且
的图象交于A(-4,a)、B两点,点B的横坐标比点A的横坐标大2,且 .
.(1)求m的值;
(2)求直线AB的解析式;
(3)指出一次函数值大于反比例函数值时x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某书店把一本新书按标价的八折出售,仍获利30%,若该书的进价为40元,则标价为_____元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,4秒后,两点相距16个单位长度.已知点B的速度是点A的速度的3倍(速度单位:单位长度/秒).
(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动4秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,再过几秒时,原点恰好处在AB的中点?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从原点O位置出发向B点运动,且C的速度是点A的速度的一半;当点C运动几秒时,C为AB的中点?

-
科目: 来源: 题型:
查看答案和解析>>【题目】用一个平面截正方体,若所得的截面是一个三角形,则留下的较大的一块几何体一定有 ( )
A. 7个面 B. 15条棱 C. 7个顶点 D. 10个顶点
-
科目: 来源: 题型:
查看答案和解析>>【题目】20160的值为( )
A.0B.1C.2016D.﹣2016
相关试题

