【题目】某小区有两段长度相等的道路需硬化,现分别由甲、乙两个工程队同时开始施工.如图的线段和折线是两队前6天硬化的道路长y甲、y乙(米)与施工时间x(天)之间的函数图象
根据图象解答下列问题:
(1)直接写出y甲、y乙(米)与x(天)之间的函数关系式.
①当0<x≤6时,y甲=;
②当0<x≤2时,y乙=;当2<x≤6时,y乙=;
(2)求图中点M的坐标,并说明M的横、纵坐标表示的实际意义;
(3)施工过程中,甲队的施工速度始终不变,而乙队在施工6天后,每天的施工速度提高到120米/天,预计两队将同时完成任务.两队还需要多少天完成任务?
参考答案:
【答案】
(1)100x;150x;50x+200
(2)解:根据题意可得: ![]()
解得: ![]()
∴M(4,400)
∴M的实际意义:在4天时,甲乙两工程队硬化道路的长度相等,均为400m 。
(3)解:设两队还需要x天完成任务,由题意可知:(120-100)x=600-500
解得:x=5
答:两队还需要5天完成任务
【解析】(1)设Y甲=KX,点(6.600)代入得到:K=100,则Y甲=100X,
0<X≤2时,设Y乙=K′X,点(2.300)代入得到:K′=150,则Y乙=150X,
2<X≤6时,设Y乙=K″X+b,
由题意得:![]()
∴ ![]()
则Y乙=50X+200.
(1)根据图像甲的工作总量与工作时间之间的函数关系式是正比例函数,设出函数关系式,用待定系数法即可得出答案;根据图像乙的工作总量与工作时间之间的函数关系式是分段函数,分别设出每一段函数关系式,用待定系数法即可得出答案;
(2)解由(1)得出的关于y甲的函数解析式与y乙的第二段函数解析式组成的方程组,求解得出方程组的解,此解就是点M的坐标;M的实际意义:在4天时,甲乙两工程队硬化道路的长度相等,均为400m ;
(3)设两队还需要x天完成任务,,由(1)知,甲的工作效率是每天修100米,根据甲前6天的工作总量+甲后期完成的工作总量=乙前6天的工作总量+乙后期完成的工作总量 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:

①抛物线与x轴的一个交点为(3,0);②函数y=ax2+bx+c的最大值为6;③抛物线的对称轴是直线
 ;④在对称轴左侧,y随x增大而增大.从上表可知,以上说法中正确的是____________.(填写序号)
;④在对称轴左侧,y随x增大而增大.从上表可知,以上说法中正确的是____________.(填写序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】若多边形的内角和大于 900°,则该多边形的边数最小为( )
A.9B.8C.7D.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:如图1,点D是△ABC外的一点,点E在BC边的延长线上,BD平分∠ABC,CD平分∠ACE.试探究∠D与∠A的数量关系.
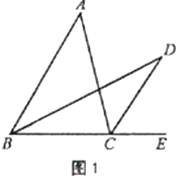
(1)特例探究:
如图2,若△ABC是等边三角形,其余条件不变,则∠D=;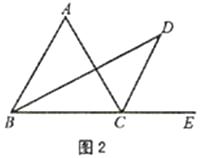
如图3,若△ABC是等腰三角形,顶角∠A=100°,其余条件不变,则∠D=;这两个图中,∠D与∠A度数的比是;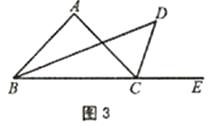
(2)猜想证明:
如图1,△ABC为一般三角形,在(1)中获得的∠D与∠A的关系是否还成立?若成立,利用图1证明你的结论;若不成立,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.2x+3y=5xy
B.(m+3)2=m2+9
C.(xy2)3=xy6
D.a10÷a5=a5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果x2+mx+4是一个完全平方公式,那么m的值是( )
A.4B.-4C.±4D.±8
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校10名篮球运动员的年龄情况,统计如下表:
年龄(岁)
12
13
14
15
人数(名)
2
4
3
1
则这10名篮球运动员年龄的中位数为( )
A.12
B.13
C.13.5
D.14
相关试题

