【题目】问题情境:如图1,点D是△ABC外的一点,点E在BC边的延长线上,BD平分∠ABC,CD平分∠ACE.试探究∠D与∠A的数量关系.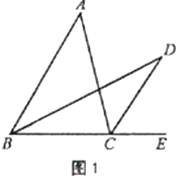
(1)特例探究:
如图2,若△ABC是等边三角形,其余条件不变,则∠D=;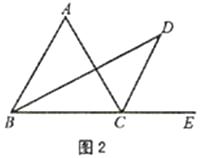
如图3,若△ABC是等腰三角形,顶角∠A=100°,其余条件不变,则∠D=;这两个图中,∠D与∠A度数的比是;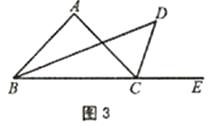
(2)猜想证明:
如图1,△ABC为一般三角形,在(1)中获得的∠D与∠A的关系是否还成立?若成立,利用图1证明你的结论;若不成立,说明理由.
参考答案:
【答案】
(1)30°;50°;1:2
(2)解:成立.
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵CD平分∠ACE,
∴∠ACD=∠DCE,
∵∠ACE是△ABC的外角,
∴∠ACE=∠ABC+∠A, 即2∠DCE =2∠DBC+∠A,
∵∠DCE是△BCD的外角,
∴∠DCE=∠DBC+∠D,
∵2∠DBC+∠A=2(∠DBC+∠D),
∴∠D= ![]() ∠A,即∠D:∠A=1:2
∠A,即∠D:∠A=1:2
【解析】解:(1)、30;50;1:2; (1)①根据角平分线的定义得出∠ABD=∠DBC=30°,∠ACD=∠DCE=60°,根据三角形的外角定理得出∠DCE=∠DBC+∠D ,从而得出∠D=30° ;②根据等腰三角形的性质得出∠ABC=40° ,根据角平分线的定义得出∠ABD=∠DBC=20°,根据三角形的外角定理得出∠ACE=∠A+∠ABC=140° ,∠ACD=∠DCE=70° ,根据三角形的外角定理得出∠DCE=∠DBC+∠D ,从而得出∠D=50° ;
(2)根据角平分线的定义得出∠ABD=∠DBC,∠ACD=∠DCE,根据三角形的外角定理得出∠ACE=∠ABC+∠A, 即2∠DCE =2∠DBC+∠A,∠DCE=∠DBC+∠D,从而得出2∠DBC+∠A=2(∠DBC+∠D),即∠D:∠A=1:2 。
-
科目: 来源: 题型:
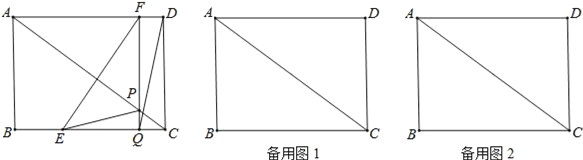
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=6cm,BC=8cm.如果点E由点B出发沿BC方向向点C匀速运动,同时点F由点D出发沿DA方向向点A匀速运动,它们的速度分别为2cm/s和1cm/s.FQ⊥BC,分别交AC、BC于点P和Q,设运动时间为t(s)(0<t<4).
(1)连结EF、DQ,若四边形EQDF为平行四边形,求t的值;
(2)连结EP,设△EPC的面积为ycm2,求y与t的函数关系式,并求y的最大值;
(3)若△EPQ与△ADC相似,请直接写出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:

①抛物线与x轴的一个交点为(3,0);②函数y=ax2+bx+c的最大值为6;③抛物线的对称轴是直线
 ;④在对称轴左侧,y随x增大而增大.从上表可知,以上说法中正确的是____________.(填写序号)
;④在对称轴左侧,y随x增大而增大.从上表可知,以上说法中正确的是____________.(填写序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】若多边形的内角和大于 900°,则该多边形的边数最小为( )
A.9B.8C.7D.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区有两段长度相等的道路需硬化,现分别由甲、乙两个工程队同时开始施工.如图的线段和折线是两队前6天硬化的道路长y甲、y乙(米)与施工时间x(天)之间的函数图象

根据图象解答下列问题:
(1)直接写出y甲、y乙(米)与x(天)之间的函数关系式.
①当0<x≤6时,y甲=;
②当0<x≤2时,y乙=;当2<x≤6时,y乙=;
(2)求图中点M的坐标,并说明M的横、纵坐标表示的实际意义;
(3)施工过程中,甲队的施工速度始终不变,而乙队在施工6天后,每天的施工速度提高到120米/天,预计两队将同时完成任务.两队还需要多少天完成任务? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.2x+3y=5xy
B.(m+3)2=m2+9
C.(xy2)3=xy6
D.a10÷a5=a5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果x2+mx+4是一个完全平方公式,那么m的值是( )
A.4B.-4C.±4D.±8
相关试题

