【题目】如图①,若抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B在抛物线L1上(点A与点B不重合),我们把这样的两抛物线L1、L2称为“伴随抛物线”,可见一条抛物线的“伴随抛物线”可以有多条.
(1)抛物线L1:y=-x2+4x-3与抛物线L2是“伴随抛物线”,且抛物线L2的顶点B的横坐标为4,求抛物线L2的表达式;
(2)若抛物线y=a1(x-m)2+n的任意一条“伴随抛物线”的表达式为y=a2(x-h)2+k,请写出a1与a2的关系式,并说明理由;
(3)在图②中,已知抛物线L1:y=mx2-2mx-3m(m>0)与y轴相交于点C,它的一条“伴随抛物线”为L2,抛物线L2与y轴相交于点D,若CD=4m,求抛物线L2的对称轴.

参考答案:
【答案】(1)y=(x-4)2-3(2)伴随抛物线的顶点不重合,∴m≠h,∴a1=-a2(3)抛物线L2的对称轴为x=±2.
【解析】试题分析:(1)先分别求得点A、点B的坐标,然后再利用待定系数法进行求解即可;
(2)根据:抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B也在抛物线L1上,可以列出两个方程,相加可得:(a1+a2 )(m-h)2=0,可得a1=-a2;
(3)易得抛物线L1的顶点坐标为(1,-4m),设抛物线L2的顶点的横坐标为h,则其纵坐标为mh2-2mh-3m,则有抛物线L2的表达式为y=-mx2+2mhx-2mh-3m,从而得点D的坐标为(0,-2mh-3m),再根据点C的坐标为(0,-3m),从而可得|(-2mh-3m)-(-3m)|=4m,解得h=±2,从而得抛物线L2的对称轴为x=±2.
试题解析:(1)由y=-x2+4x-3可得A的坐标为(2,1),
将x=4代入y=-x2+4x-3,得y=-3,∴B的坐标为(4,-3),
设抛物线L2的解析式为y=a(x-4)2-3; 将(2,1)代入y=a(x-4)2-3,
得1=a(2-4)2-3,解得a=1,
∴抛物线L2的表达式为y=(x-4)2-3;
(2)a1=-a2,理由如下:
∵抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B在抛物线L1上,
∴可列方程组:  ,
,
整理,得(a1+a2)(m-h)2=0,
∵伴随抛物线的顶点不重合,∴m≠h,∴a1=-a2;
(3)抛物线L1:y=mx2-2mx-3m的顶点坐标为(1,-4m),
设抛物线L2的顶点的横坐标为h,则其纵坐标为mh2-2mh-3m,
∴抛物线L2的表达式为y=-m(x-h)2+mh2-2mh-3m,
化简得,y=-mx2+2mhx-2mh-3m,
所以点D的坐标为(0,-2mh-3m),
又点C的坐标为(0,-3m),
可得|(-2mh-3m)-(-3m)|=4m, 解得h=±2,
∴抛物线L2的对称轴为x=±2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,无论k取何实数,直线y=(k-1)x+4-5k总经过定点P,则点P与动点Q(5m-1,5m+1)的距离的最小值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据市卫生防疫部门的要求,游泳池必须定期换水后才能对外开放.在换水时需要经“排水—清冼—灌水”的过程.某游泳馆从早上7:00开始对游泳池进行换水,已知该游泳池的排水速度是灌水速度的1.6倍,其中游泳池内剩余的水量y(m3)与换水时间x(h)之间的函数图象如图所示,根据图象解答下列问题:
(1)填空:该游泳池清洗需要 小时;
(2)求排水过程中的y(m3)与x(h)之间的函数关系式,并写出自变量x的取值范围;
(3)若该游泳馆在换水结束后30分钟才能对外开放,试问游泳爱好者小明能否在中午12:40进入该游泳馆游泳?

-
科目: 来源: 题型:
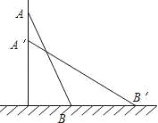
查看答案和解析>>【题目】如图,一架梯子AB长13米,斜靠在一面墙上,梯子底端离墙5米.(1)这个梯子的顶端距地面有多高?(2)如果梯子的顶端下滑了5米,那么梯子的底端在水平方向滑动了多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,直线y=-2x+1与y轴交于点C,直线y=x+k(k≠0)与y轴交于点A,与直线y=-2x+1交于点B,设点B的横坐标为x0.
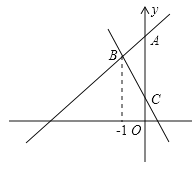
(1)如图,若x0=-1.
①求点B的坐标及k的值;
②求直线y=-2x+1、直线y=x+k与y轴所围成的△ABC的面积;
(2)若-2<x0<-1,求整数k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=2x+b.
(1)它的图像与两坐标轴所围成的图形的面积等于4,求b的值;
(2)它的图像经过一次函数y=-2x+1、y=x+4图像的交点,求b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售A型和B型两种电脑,其中A型电脑每台的利润为400元,B型电脑每台的利润为500元.该商店计划再一次性购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y关于x的函数关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大利润是多少?
(3)实际进货时,厂家对A型电脑出厂价下调a(0<a<200)元,且限定商店最多购进A型电脑60台,若商店保持同种电脑的售价不变,请你根据以上信息,设计出使这100台电脑销售总利润最大的进货方案.
相关试题

