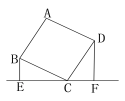
【题目】如图,四边形ABCD是正方形,BE⊥EF,DF⊥EF,BE=2.5cm,DF=4cm,那么EF的长为( )
A. 6.5cm B. 6cm C. 5.5cm D. 4cm
参考答案:
【答案】A
【解析】
根据已知条件易证△BCE≌△CDF,再根据全等三角形的性质得到CE=DF,BE=CF,由EF=EC+CF即可求得EF的长.
∵四边形ABCD是正方形,
∴∠BCD=90°,BC=CD.
又∵BE⊥EF,DF⊥EF,
∴∠BEC=∠CFD=90°,
∵∠CBE+∠ECB=90°,∠DCF+∠ECB=90°,
∴∠CBE=∠DCF,
在△BCE与△CDF中,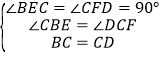 ,
,
∴△BCE≌△CDF(AAS),
∴CE=DF,BE=CF,
又∵BE=2.5cm,DF=4cm,
∴EF=EC+CF=DF+BE=6.5cm.
故选A.
-
科目: 来源: 题型:
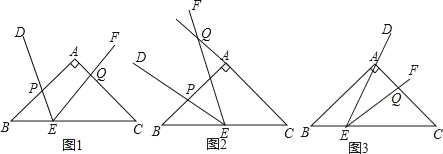
查看答案和解析>>【题目】如图1,在等腰直角△ABC中,∠BAC=90°,AB=AC=2,点E是BC边上一点,∠DEF=45°且角的两边分别与边AB,射线CA交于点P,Q.
(1)如图2,若点E为BC中点,将∠DEF绕着点E逆时针旋转,DE与边AB交于点P,EF与CA的延长线交于点Q.设BP为x,CQ为y,试求y与x的函数关系式,并写出自变量x的取值范围;
(2)如图3,点E在边BC上沿B到C的方向运动(不与B,C重合),且DE始终经过点A,EF与边AC交于Q点.探究:在∠DEF运动过程中,△AEQ能否构成等腰三角形,若能,求出BE的长;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰
 中,
中,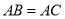 ,
,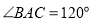 ,
, 于点
于点 ,点
,点 是
是 延长线上一点,点
延长线上一点,点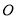 是线段
是线段 上一点,
上一点, .下列结论:①
.下列结论:①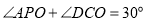 ;②
;②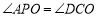 ;③
;③ 是等边三角形;④
是等边三角形;④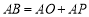 .其中正确结论的个数是( )
.其中正确结论的个数是( )
A.1B.
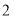 C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=
 x2+bx+c的图象经过点A(﹣3,6),并与x轴交于点B(﹣1,0)和点C,与y轴交于点E,顶点为P,对称轴与x轴交于点D
x2+bx+c的图象经过点A(﹣3,6),并与x轴交于点B(﹣1,0)和点C,与y轴交于点E,顶点为P,对称轴与x轴交于点D(Ⅰ)求这个二次函数的解析式;
(Ⅱ)连接CP,△DCP是什么特殊形状的三角形?并加以说明;
(Ⅲ)点Q是第一象限的抛物线上一点,且满足∠QEO=∠BEO,求出点Q的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形ABCD的边长为4cm,∠A=120°,则菱形ABCD的面积为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中秋节吃月饼是中华民族的传统习俗.节日期间,小丽家买了三种不同馅的月饼,分别是:五仁月饼(记为A),豆沙月饼(记为B),草莓月饼(记为C),这些月饼除了馅不同,其余均相同.妈妈剪开包装袋,给一个白盘中放入了两个五仁月饼,一个豆沙月饼和一个草莓月饼;给一个花盘中放入了两个草莓月饼,一个五仁月饼和一个豆沙月饼.若小丽先从白盘里的四个月饼中随机取一个月饼,再从花盘里的四个月饼中随机取一个月饼,请用列表法或画树状图的方法,求小丽取到的两个月饼中一个是五仁月饼、一个是豆沙月饼的概率.
-
科目: 来源: 题型:
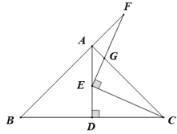
查看答案和解析>>【题目】如图,Rt△ABC 中,AB=AC,∠BAC=90°,AD 是 BC 边上的高,E 是 AD 上的一点。连接 EC,过点 E 作 EF⊥EC 交射线 BA 于点 F,EF、AC 交于点 G。若 DE=3,△EGC 与△AFG 面积的差是 2,则 BD=_____.
相关试题

