【题目】如图,等腰![]() 中,
中,![]() ,
,![]() ,
,![]() 于点
于点![]() ,点
,点![]() 是
是![]() 延长线上一点,点
延长线上一点,点![]() 是线段
是线段![]() 上一点,
上一点,![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() 是等边三角形;④
是等边三角形;④![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )

A.1B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】D
【解析】
①②连接OB,根据垂直平分线性质即可求得OB=OC=OP,即可解题;
③根据周角等于360°和三角形内角和为180°即可求得∠POC=2∠ABD=60°,即可解题;
④AB上找到Q点使得AQ=OA,易证△BQO≌△PAO,可得PA=BQ,即可解题.
连接![]() ,
,
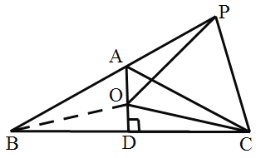
∵![]() ,AD⊥BC,
,AD⊥BC,
∴![]() 是
是![]() 垂直平分线,
垂直平分线,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵AB=AC,∠BAC=120
∴![]()
∴![]() ,
,
∴![]() .
.
故①②正确;
∵![]() 中,
中,![]() ,
,
![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
故③正确;
在AB上找到Q点使得AQ=OA,
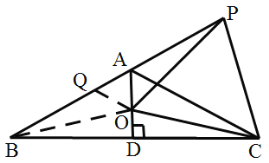
则![]() 为等边三角形,
为等边三角形,
则![]() ,
,
在![]() 和
和![]() 中,
中,
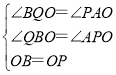
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,故④正确.
,故④正确.
故选:D.
-
科目: 来源: 题型:
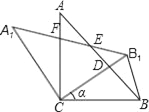
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AC=BC=1,将△ABC绕点C逆时针旋转得到△A1B1C,旋转角为ɑ(0°<ɑ<90°),连接BB1.设CB1交AB于点D,A1B1分别交AB、AC于点E,F.
(1)求证:△BCD≌△A1CF;
(2)若旋转角ɑ为30°,
①请你判断△BB1D的形状;
②求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知直线
 与直线
与直线 相交于点
相交于点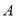 。
。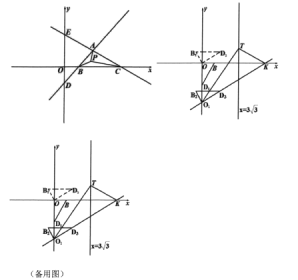
(1)求点
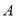 的坐标;
的坐标;(2)点
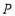 是
是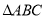 内部一点,连接
内部一点,连接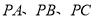 ,求
,求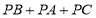 的最小值;
的最小值;(3)将点
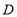 向下平移一个单位得到点
向下平移一个单位得到点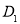 ,连接
,连接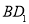 ,将
,将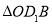 绕点
绕点 旋转至
旋转至 的位置,使
的位置,使 轴,再将
轴,再将 沿
沿 轴上下平移得到
轴上下平移得到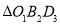 ,在平移过程中,直线
,在平移过程中,直线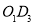 与
与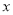 轴交于点
轴交于点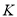 ,在直线
,在直线 上任取一点
上任取一点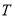 ,连接
,连接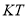 ,
,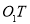 ,
, 能否以
能否以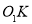 为直线边构成等腰直角三角形?若能,请直接写出所有符合条件的
为直线边构成等腰直角三角形?若能,请直接写出所有符合条件的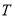 点的坐标,若不能,请说明理由。
点的坐标,若不能,请说明理由。 -
科目: 来源: 题型:
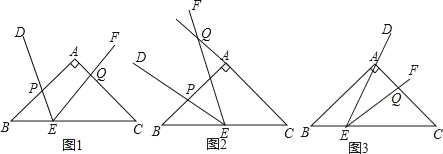
查看答案和解析>>【题目】如图1,在等腰直角△ABC中,∠BAC=90°,AB=AC=2,点E是BC边上一点,∠DEF=45°且角的两边分别与边AB,射线CA交于点P,Q.
(1)如图2,若点E为BC中点,将∠DEF绕着点E逆时针旋转,DE与边AB交于点P,EF与CA的延长线交于点Q.设BP为x,CQ为y,试求y与x的函数关系式,并写出自变量x的取值范围;
(2)如图3,点E在边BC上沿B到C的方向运动(不与B,C重合),且DE始终经过点A,EF与边AC交于Q点.探究:在∠DEF运动过程中,△AEQ能否构成等腰三角形,若能,求出BE的长;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=
 x2+bx+c的图象经过点A(﹣3,6),并与x轴交于点B(﹣1,0)和点C,与y轴交于点E,顶点为P,对称轴与x轴交于点D
x2+bx+c的图象经过点A(﹣3,6),并与x轴交于点B(﹣1,0)和点C,与y轴交于点E,顶点为P,对称轴与x轴交于点D(Ⅰ)求这个二次函数的解析式;
(Ⅱ)连接CP,△DCP是什么特殊形状的三角形?并加以说明;
(Ⅲ)点Q是第一象限的抛物线上一点,且满足∠QEO=∠BEO,求出点Q的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,BE⊥EF,DF⊥EF,BE=2.5cm,DF=4cm,那么EF的长为( )
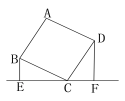
A. 6.5cm B. 6cm C. 5.5cm D. 4cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形ABCD的边长为4cm,∠A=120°,则菱形ABCD的面积为______.
相关试题

