Question

【题目】如图，在四边形ABCD中，AD∥BC，AD=5cm，BC=9cm．M是CD的中点，P是BC边上的一动点（P与B，C不重合），连接PM并延长交AD的延长线于Q．

（1）试说明△PCM≌△QDM．

（2）当点P在点B、C之间运动到什么位置时，四边形ABPQ是平行四边形？并说明理由．

Answer 1

【答案】（1）证明见解析;（2）PC=2,理由见解析.

【解析】试题分析: （1）要证明△PCM≌△QDM，可以根据两个三角形全等四个定理，即AAS、ASA、SAS、SSS中的ASA．利用∠QDM=∠PCM，DM=CM，∠DMQ=∠CMP即可得出；

（2）得出P在B、C之间运动的位置，根据一组对边平行且相等的四边形是平行四边形得出．

试题解析:

（1）∵AD∥BC，∴∠QDM=∠PCM.

∵M是CD的中点，∴DM=CM，∵∠DMQ=∠CMP，

在△PCM和△QDM中，∵，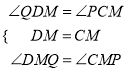

∴△PCM≌△QDM（ASA）．

（2）当四边形ABPQ是平行四边形时，PB=AQ，

∵BC﹣CP=AD+QD，∴9﹣CP=5+CP，∴CP=（9﹣5）÷2=2．

∴当PC=2时，四边形ABPQ是平行四边形．

点睛:本题中和考查全等三角形、平行四边形的判定,熟练掌握平行四边形的性质和判定方法是解题的关键.