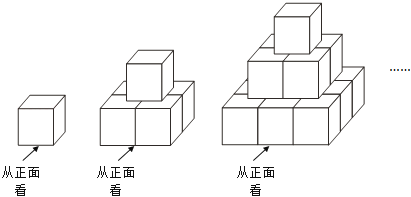
【题目】现用棱长为1cm的若干小立方体,按如图所示的规律在地上搭建若个几何体.图中每个几何体自上而下分别叫第一层,第二层…第n层(n为正整数),其中第一层摆放一个小立方体,第二层摆放4个小立方体,第三层摆放9个小立方体…,依次按此规律继续摆放.
(1)求搭建第4个几何体需要的小立方体个数;
(2)为了美观,若将每个几何体的所有露出部分(不包含底面)都喷涂油漆,已知喷涂1cm2需要油漆0.2g.
①求喷涂第4个几何体需要油漆多少g?
②求喷涂第n个几何体需要油漆多少g?(用含n的代数式表示)
参考答案:
【答案】(1)30;(2)①11.2(g).②(0.6n2+0.4n)g.
【解析】
试题分析:(1)观察得到每层向上的面都为正方形,即每层的个数都为平方数,则搭建第4个几何体的小立方体的个数=1+4+9+16;第n个几何体第n层的个数为n2,所以总数为1+22+32+42+…+n2;
(2)①喷漆第四个几何露在外面的表面积为:4×(1+2+3+4)+42=56(cm2),再用表面积×0.2,即可解答.
②第n个几何体的所有露出部分(不含底面)的面积=4×(1+2+3+…+n)+n2,化简后乘以0.2即可.
解:(1)搭建第4个几何体的小立方体的个数=1+4+9+16=30;
(2)①喷漆第四个几何露在外面的表面积为:4×(1+2+3+4)+42=56(cm2),
56×0.2=11.2(g).
②第n个几何体的所有露出部分(不含底面)的面积=4×(1+2+3+…+n)+n2=4×![]() +n2=3n2+2n,
+n2=3n2+2n,
所以所需要的油漆量=(3n2+2n)×0.2=(0.6n2+0.4n)g.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A为⊙O外一点,连结OA交⊙O于P,AB为⊙O的切线,B为切点,AP=5㎝,AB=
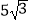 ㎝,则劣弧
㎝,则劣弧 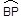 与AB,AP所围成的阴影的面积是.
与AB,AP所围成的阴影的面积是.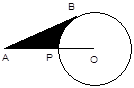
-
科目: 来源: 题型:
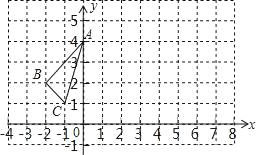
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)将△ABC向右平移6个单位,作出平移后的△A1B1C1,并写出△A1B1C1各顶点的坐标;
(2)在y轴上是否存在点M,使得CM+BM最小?若存在,求出点M坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学进行社会调查,随机抽查了某个地区的20个家庭的收入情况,并绘制了统计图,请你根据统计图给出的信息回答:

(1)填写完成下表:
年收入(万元)
0.6
0.9
1.0
1.1
1.2
1.3
1.4
9.7
户 数
1
1
2
4
这20个家庭的年平均收入为 万元;
(2)样本中的中位数是 万元,众数是 万元;
(3)在平均数、中位数两数中, 更能反映这个地区家庭的年收入水平.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1 , O2 , O3 , … 组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒
 个单位长度,则第2016秒时,点P的坐标是
个单位长度,则第2016秒时,点P的坐标是
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式(2x2+ax﹣y+6)﹣(2bx2﹣3x+5y﹣1).
(1)若多项式的值与字母x的取值无关,求a、b的值.
(2)在(1)的条件下,先化简多项式3(a2﹣ab+b2)﹣(3a2+ab+b2),再求它的值.
(3)在(1)的条件下,求(b+a2)+(2b+
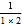 a2)+(3b+
a2)+(3b+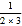 a2)+…+(9b+
a2)+…+(9b+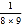 a2)的值.
a2)的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,
 的三个顶点坐标分别为A(2,-4),B(3,-2), C(6,-3).
的三个顶点坐标分别为A(2,-4),B(3,-2), C(6,-3).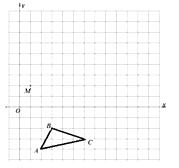
①画出△ABC关于 轴对称的△A1B1C1;
轴对称的△A1B1C1;
②以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2 , 使△A2B2C2与△A1B1C1的相似比为2︰1.
相关试题

