【题目】如图,已知A为⊙O外一点,连结OA交⊙O于P,AB为⊙O的切线,B为切点,AP=5㎝,AB= ![]() ㎝,则劣弧
㎝,则劣弧 ![]() 与AB,AP所围成的阴影的面积是.
与AB,AP所围成的阴影的面积是.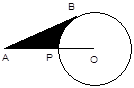
参考答案:
【答案】![]()
【解析】连接OB,因为AB是⊙O的切线,
所以∠ABO=90°;
设⊙O的半径为r.由勾股定理得:(5+r)2=( ![]() )2+r2,
)2+r2,
解得r=5cm;在Rt△ABO中,AO=10cm,OB=OP=5cm,
因此∠BOP=60°;
∴S=S△AOB-S扇形OBP= ![]() (cm2).
(cm2).
【考点精析】通过灵活运用勾股定理的概念和切线的性质定理,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两城相距800千米,一辆客车从甲城开往乙城,车速为
 千米
千米 小时,同时一辆出租车从乙城开往甲城,车速为90千米
小时,同时一辆出租车从乙城开往甲城,车速为90千米 小时,设客车行驶时间为
小时,设客车行驶时间为 小时
小时
 当
当 时,客车与乙城的距离为多少千米
时,客车与乙城的距离为多少千米 用含a的代数式表示
用含a的代数式表示
 已知
已知 ,丙城在甲、乙两城之间,且与甲城相距260千米
,丙城在甲、乙两城之间,且与甲城相距260千米 求客车与出租车相距100千米时客车的行驶时间;
求客车与出租车相距100千米时客车的行驶时间; 列方程解答
列方程解答
 已知客车和出租车在甲、乙之间的服务站M处相遇时,出租车乘客小王突然接到开会通知,需要立即返回,此时小王有两种返回乙城的方案:
已知客车和出租车在甲、乙之间的服务站M处相遇时,出租车乘客小王突然接到开会通知,需要立即返回,此时小王有两种返回乙城的方案:方案一:继续乘坐出租车到丙城,加油后立刻返回乙城,出租车加油时间忽略不计;
方案二:在M处换乘客车返回乙城.
试通过计算,分析小王选择哪种方案能更快到达乙城?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若两个扇形满足弧长的比等于它们半径的比,则称这两个扇形相似。如图,如果扇形AOB与扇形
 是相似扇形,且半径
是相似扇形,且半径  (
(  为不等于0的常数)。那么下面四个结论:①∠AOB=∠
为不等于0的常数)。那么下面四个结论:①∠AOB=∠  ;②△AOB∽△
;②△AOB∽△  ;③
;③  ;④扇形AOB与扇形
;④扇形AOB与扇形  的面积之比为
的面积之比为  。成立的个数为:( )
。成立的个数为:( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把直线y=﹣2x向上平移后,分别交y轴、x轴于A、B两点,直线AB经过点(m,n)且2m+n=6,则点O到线段AB的距离为_____.

-
科目: 来源: 题型:
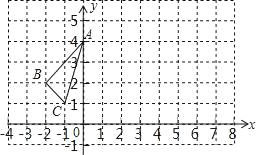
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)将△ABC向右平移6个单位,作出平移后的△A1B1C1,并写出△A1B1C1各顶点的坐标;
(2)在y轴上是否存在点M,使得CM+BM最小?若存在,求出点M坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学进行社会调查,随机抽查了某个地区的20个家庭的收入情况,并绘制了统计图,请你根据统计图给出的信息回答:

(1)填写完成下表:
年收入(万元)
0.6
0.9
1.0
1.1
1.2
1.3
1.4
9.7
户 数
1
1
2
4
这20个家庭的年平均收入为 万元;
(2)样本中的中位数是 万元,众数是 万元;
(3)在平均数、中位数两数中, 更能反映这个地区家庭的年收入水平.
-
科目: 来源: 题型:
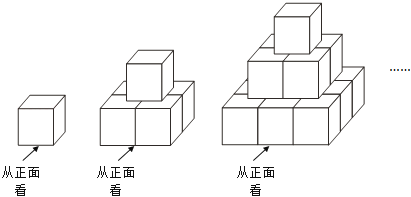
查看答案和解析>>【题目】现用棱长为1cm的若干小立方体,按如图所示的规律在地上搭建若个几何体.图中每个几何体自上而下分别叫第一层,第二层…第n层(n为正整数),其中第一层摆放一个小立方体,第二层摆放4个小立方体,第三层摆放9个小立方体…,依次按此规律继续摆放.
(1)求搭建第4个几何体需要的小立方体个数;
(2)为了美观,若将每个几何体的所有露出部分(不包含底面)都喷涂油漆,已知喷涂1cm2需要油漆0.2g.
①求喷涂第4个几何体需要油漆多少g?
②求喷涂第n个几何体需要油漆多少g?(用含n的代数式表示)
相关试题

