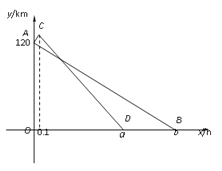
【题目】(本题满分10分)从M地到N地有一条普通公路,总路程为120km;有一条高速公路,总路程为126km.甲车和乙车同时从M地开往N地,甲车全程走普通公路,乙车先行驶了另一段普通公路,然后再上高速公路.假设两车在普通公路和高速公路上分别保持匀速行驶,其中在普通公路上的行车速度为60km/h,在高速公路上的行车速度为100km/h.设两车出发x h时,距N地的路程为y km,图中的线段AB与折线ACD分别表示甲车与乙车的y与x之间的函数关系.
(1)填空:a= ,b= ;
(2)求线段AB、CD所表示的y与x之间的函数关系式;
(3)两车在何时间段内离N地的路程之差达到或超过30km?
参考答案:
【答案】(1)1.36,2;(2)y1=﹣60x+120;y2=﹣100x+136;
(3)当1.15≤x≤1.5时,两车离N地的路程之差达到或超过30km.
【解析】试题分析:(1)求出C坐标,再根据时间=路程÷速度分别求出甲车在普通公路上行驶的时间及乙车在高速公路上行驶的时间,可得a、b的值;
(2)根据A、B、C、D四点坐标待定系数法求解可得线段AB、CD所表示的y与x之间的函数关系式;
(3)分类讨论:当0<x<0.1时,由解析式可知甲、乙两车距离差最大为12;当0.1≤x<1.36时,由y1﹣y2≥30列不等式可得x的范围;当1.36≤x≤2时,由y1≥30列不等式可得此时x的范围,综合以上三种情况可得答案.
试题解析:(1)根据题意,知:点C的坐标为(0.1,126),
∴a=0.1+![]() =1.36,b=
=1.36,b=![]() =2,
=2,
故答案为:1.36,2.
(2)设线段AB所表示的y与x之间的函数关系式分别为y1=k1x+b1,
将A(0,120)、B(2,0)的坐标代入得:
![]() ,
,
解得: ![]() ,
,
∴y1=﹣60x+120;
设线段CD所表示的y与x之间的函数关系式分别为y2=k2x+b2,
将C(0.1,126)、D(1.36,0)的坐标代入得:
![]() ,
,
解得: ![]() ,
,
∴y2=﹣100x+136.
(3)由题意,①当x=0.1时,两车离N地的路程之差是12km,
∴当0<x<0.1时,两车离N地的路程之差不可能达到或超过30km.
②当0.1≤x<1.36时,由y1﹣y2≥30,得(﹣60x+120)﹣(﹣100x+136)≥30,
解得x≥1.15.
即当1.15≤x<1.36时,两车离N地的路程之差达到或超过30km.
③当1.36≤x≤2时,由y1≥30,得﹣60x+120≥30,解得x≤1.5.
即当1.36≤x≤1.5时,两车离N地的路程之差达到或超过30km.
综上,当1.15≤x≤1.5时,两车离N地的路程之差达到或超过30km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知﹣2am﹣2b4与3abn+2是同类项,则(n﹣m)m= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】中考体育测试前,某区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽测了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图:
请你根据图中的信息,解答下列问题:
(
 )写出扇形图中
)写出扇形图中 __________
__________ ,并补全条形图.
,并补全条形图.(
 )在这次抽测中,测试成绩的众数和中位数分别是__________个、__________个.
)在这次抽测中,测试成绩的众数和中位数分别是__________个、__________个.(
 )该区体育中考选报引体向上的男生共有
)该区体育中考选报引体向上的男生共有 人,如果体育中考引体向上达
人,如果体育中考引体向上达 个以上(含
个以上(含 个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?
个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=5,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).
请回答:BC+DE的值为
参考小明思考问题的方法,解决问题:
如图3,已知ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数 -
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2=2x的解是( )
A.2B.0C.2或0D.﹣2或0
-
科目: 来源: 题型:
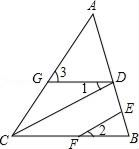
查看答案和解析>>【题目】如图,已知,CD∥EF,∠1=∠2,求证:∠3=∠ACB.请补全证明过程.
证明:∵CD∥EF,( )
∴∠2=∠DCB,(两直线平行,同位角相等)
∵∠1=∠2,( )
∴∠1=∠DCB,( )
∴GD∥CB,( )
∴∠3=∠ACB,( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解一元二次方程x2﹣2x=5的过程中,配方正确的是( )
A.(x+1)2=6B.(x﹣1)2=6C.(x+2)2=9D.(x﹣2)2=9
相关试题

