【题目】《代数学》中记载,形如x2+10x=39的方程,求正数解的几何方法是:“如图1,先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为![]() x的矩形,得到大正方形的面积为39+25=64,则该方程的正数解为8-5=3”,小聪按此方法解关于x的方程x2+6x+m=0时,构造出如图2所示的图形,己知阴影部分的面积为36,则该方程的正数解为( )
x的矩形,得到大正方形的面积为39+25=64,则该方程的正数解为8-5=3”,小聪按此方法解关于x的方程x2+6x+m=0时,构造出如图2所示的图形,己知阴影部分的面积为36,则该方程的正数解为( )

A.6B.3![]() -3C.3
-3C.3![]() -2D.3
-2D.3![]() -
-![]()
参考答案:
【答案】B
【解析】
根据题意列方程,即x2+6x就是阴影部分的面积,用配方法解二次方程,取正数解即可.
解: 由题意得:x2+6x=36,
解方程得:x2+2×3x+9=45,
(x+3)2=45
∴x+3=3![]() , 或x+3=-3
, 或x+3=-3![]() ,
,
∴x=3![]() -3, 或x=-3
-3, 或x=-3![]() -3<0,
-3<0,
∴该方程的正数解为:3![]() -3,
-3,
故答案为:B
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解本校七年级学生数学学习情况,随机抽查该年级若干名学生进行测试,然后把测试结果分为
 个等级:
个等级: ,并将统计结果绘制成两幅不完整的统计图,请根据图中的信息解答下列问题:
,并将统计结果绘制成两幅不完整的统计图,请根据图中的信息解答下列问题:
 补全条形统计图;
补全条形统计图; 等级为
等级为 等的所在扇形的圆心角是 度;
等的所在扇形的圆心角是 度; 如果七年级共有学生
如果七年级共有学生 名,请估算该年级学生中数学学习为
名,请估算该年级学生中数学学习为 等和
等和 等的共多少人?
等的共多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以直线AB上一点O为端点作射线OC,使∠AOC=65°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图①,若直角三角板DOE的一边OD放在射线OA上,则∠COE= ;
(2)如图②,将直角三角板DOE绕点O顺时针方向转动到某个位置,若OC恰好平分∠AOE,求∠COD的度数;
(3)如图③,将直角三角板DOE绕点O任意转动,如果OD始终在∠AOC的内部,试猜想∠AOD和∠COE有怎样的数量关系?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(1,0),B(2,0),C(0,﹣2),直线x=m(m>2)与x轴交于点D.
(1)求二次函数的解析式;
(2)在直线x=m(m>2)上有一点E(点E在第四象限),使得E、D、B为顶点的三角形与以A、O、C为顶点的三角形相似,求E点坐标(用含m的代数式表示);
(3)在(2)成立的条件下,抛物线上是否存在一点F,使得四边形ABEF为平行四边形?若存在,请求出F点的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B分别在x轴、y轴上,点O关于AB的对称点C在第一象限,将△ABC沿x轴正方向平移k个单位得到△DEF(点B与E是对应点),点F落在双曲线y=
 上,连结BE交该双曲线于点G.∠BAO=60°,OA=2GE,则k的值为 ________ .
上,连结BE交该双曲线于点G.∠BAO=60°,OA=2GE,则k的值为 ________ . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】为鼓励居民节约用电,某市采用价格调控手段达到省电目的.该市电费收费标准如下表(按月结算) :
每月用电量/度
电价/(元/度)
不超过
 度的部分
度的部分 元/度
元/度超过
 度且不超过
度且不超过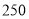 度的部分
度的部分 元/度
元/度超过
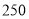 度的部分
度的部分 元/度
元/度解答下列问题:
(1)某居民
 月份用电量为
月份用电量为 度,请问该居民
度,请问该居民 月应缴电费多少元?
月应缴电费多少元?(2)设某月的用电量为
 度
度 ,试写出不同用电量范围应缴的电费(用
,试写出不同用电量范围应缴的电费(用 表示) .
表示) .(3)某居民
 月份缴电费
月份缴电费 元,求该居民
元,求该居民 月份的用电量.
月份的用电量. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国的国球是乒乓球,世界上乒乓球板的拍形大体上可以归为三类:圆形、方形和异形,绝大多数的横板与中国式的直板都是圆型的.如图,李明同学自制一块乒乓球拍,正面是半径为8 cm的⊙O,弧AB的长为4πcm,弓形ACB(阴影部分)粘贴胶皮,则胶皮面积为( )

A. (32+48π)cm2 B. (16π﹣32)cm2 C. 64πcm2 D. (48π﹣32)cm2
相关试题

