【题目】我国的国球是乒乓球,世界上乒乓球板的拍形大体上可以归为三类:圆形、方形和异形,绝大多数的横板与中国式的直板都是圆型的.如图,李明同学自制一块乒乓球拍,正面是半径为8 cm的⊙O,弧AB的长为4πcm,弓形ACB(阴影部分)粘贴胶皮,则胶皮面积为( )

A. (32+48π)cm2 B. (16π﹣32)cm2 C. 64πcm2 D. (48π﹣32)cm2
参考答案:
【答案】A
【解析】分析:连接OA、OB,根据三角形的面积公式求出S△AOB,根据扇形面积公式求出扇形ACB的面积,计算即可.
详解:连接OA、OB,
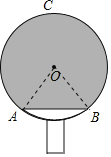
设∠AOB的度数为n°,
∵![]() 的长为4πcm,
的长为4πcm,
∴![]() =4π,
=4π,
∴n=90
∴∠AOB=90°,
∴S△AOB=![]() ×8×8=32,
×8×8=32,
扇形ACB(阴影部分)=![]() =48π,
=48π,
则弓形ACB胶皮面积为(32+48π)cm2,
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】《代数学》中记载,形如x2+10x=39的方程,求正数解的几何方法是:“如图1,先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为
 x的矩形,得到大正方形的面积为39+25=64,则该方程的正数解为8-5=3”,小聪按此方法解关于x的方程x2+6x+m=0时,构造出如图2所示的图形,己知阴影部分的面积为36,则该方程的正数解为( )
x的矩形,得到大正方形的面积为39+25=64,则该方程的正数解为8-5=3”,小聪按此方法解关于x的方程x2+6x+m=0时,构造出如图2所示的图形,己知阴影部分的面积为36,则该方程的正数解为( ) 
A.6B.3
 -3C.3
-3C.3 -2D.3
-2D.3 -
-
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B分别在x轴、y轴上,点O关于AB的对称点C在第一象限,将△ABC沿x轴正方向平移k个单位得到△DEF(点B与E是对应点),点F落在双曲线y=
 上,连结BE交该双曲线于点G.∠BAO=60°,OA=2GE,则k的值为 ________ .
上,连结BE交该双曲线于点G.∠BAO=60°,OA=2GE,则k的值为 ________ . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】为鼓励居民节约用电,某市采用价格调控手段达到省电目的.该市电费收费标准如下表(按月结算) :
每月用电量/度
电价/(元/度)
不超过
 度的部分
度的部分 元/度
元/度超过
 度且不超过
度且不超过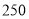 度的部分
度的部分 元/度
元/度超过
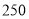 度的部分
度的部分 元/度
元/度解答下列问题:
(1)某居民
 月份用电量为
月份用电量为 度,请问该居民
度,请问该居民 月应缴电费多少元?
月应缴电费多少元?(2)设某月的用电量为
 度
度 ,试写出不同用电量范围应缴的电费(用
,试写出不同用电量范围应缴的电费(用 表示) .
表示) .(3)某居民
 月份缴电费
月份缴电费 元,求该居民
元,求该居民 月份的用电量.
月份的用电量. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD。理由如下:

∵∠1=∠2(已知)
且∠1=∠4( )
∴∠2=∠4(等量代换)
∴CE∥BF( )
∴∠ =∠BFD( )
又∵∠B=∠C(已知)
∴ (等量代换)
∴AB∥CD( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.

(1)求证:△ADE≌△CFE;
(2)若GB=2,BC=4,BD=1,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与双曲线相交于点A(m,3),与x轴交于点C.
与双曲线相交于点A(m,3),与x轴交于点C. (1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.

相关试题

