【题目】已知多项式2x3y﹣xy+16的次数为a,常数项为b,a,b分别对应着数轴上的A、B两点.
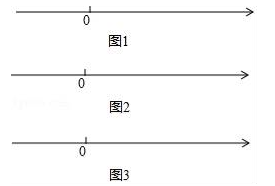
(1)a= ,b= ;并在数轴上画出A、B两点;
(2)若点P从点A出发,以每秒3个单位长度单位的速度向x轴正半轴运动,求运动时间为多少时,点P到点A的距离是点P到点B的距离的2倍;
(3)数轴上还有一点C的坐标为30,若点P和Q同时从点A和点B出发,分别以每秒3个单位长度和每秒1个单位长度的速度向C点运动,P到达C点后,再立即以同样的速度返回,运动的终点A,求点P和点Q运动多少秒时,P,Q两点之间的距离为4,并求出此时点Q的坐标.
参考答案:
【答案】(1)4,16;(2)![]() 或8秒;(3)点P和点Q运动多4或8或9或11秒时,P,Q两点之间的距离为4.
或8秒;(3)点P和点Q运动多4或8或9或11秒时,P,Q两点之间的距离为4.
【解析】试题分析:(1)根据多项式的次数,及常数项的定义就可以得出结论,就可以求出A、B所表示的数,进而在数轴上表示即可;
(2)设运动时间为ts,由题意:3t=2(16﹣4﹣3t)或3t=2(4+3t﹣16),解方程即可得;
(3)设运动时间为ts,由题意:12+t﹣3t=4或3t﹣(12+t)=4或12+t+4+3t=52或12+t+3t﹣4=52,解方程即可得.
试题解析:(1)∵多项式2x3y﹣xy+16的次数为a,常数项为 b,
∴a=4,b=16,
故答案为4,16.
点A、B的位置如图所示.
![]()
(2)设运动时间为ts,
由题意:3t=2(16﹣4﹣3t)或3t=2(4+3t﹣16),
解得t=![]() 或8,
或8,
∴运动时间为![]() 或8秒时,点 P到点A的距离是点P到点B的距离的2倍;
或8秒时,点 P到点A的距离是点P到点B的距离的2倍;
(3)设运动时间为ts,
由题意:12+t﹣3t=4或3t﹣(12+t)=4或12+t+4+3t=52或12+t+3t﹣4=52,
解得t=4或8或9或11,
∴点P和点Q运动时间为4或8或9或11秒时,P,Q两点之间的距离为4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠1=18°18′,∠2=18.18°,∠3=18.3°,下列结论正确的是( )
A.∠1=∠3
B.∠1=∠2
C.∠2=∠3
D.∠1=∠2=∠3 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件:①经过有交通信号灯的路口,遇到红灯;②掷一枚均匀的正方体骰子,骰子落地后朝上的点数不是奇数便是偶数;③长为5cm、5cm、11cm的三条线段能围成一个三角形;④买一张体育彩票中奖。其中随机事件有( )
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D,那么∠ADC的度数为( )

A.120°
B.30°
C.60°
D.80° -
科目: 来源: 题型:
查看答案和解析>>【题目】在“宏扬传统文化,打造书香校园”活动中,学校计划开展四项活动:“A﹣国学诵读”、“B﹣演讲”、“C﹣课本剧”、“D﹣书法”,要求每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如下:
(1)如图,希望参加活动C占20%,希望参加活动B占15%,则被调查的总人数为 人,扇形统计图中,希望参加活动D所占圆心角为 度,根据题中信息补全条形统计图.
(2)学校现有800名学生,请根据图中信息,估算全校学生希望参加活动A有多少人?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠1与∠2互余,∠2与∠3互补,∠1=58°,则∠3=( )
A.58°
B.148°
C.158°
D.32° -
科目: 来源: 题型:
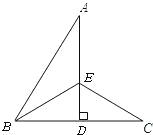
查看答案和解析>>【题目】如图,∠ABC=50°,AD垂直且平分BC于点D,∠ABC的平分线BE交AD于点E,连接EC,则∠AEC的度数是( )
A.50°
B.25°
C.80°
D.115°
相关试题

