【题目】为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.下表是该市民一户一表"生活用水阶梯式计费价格表的部分信息:
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
|
|
|
超过 |
|
|
超过 |
|
|
(说明:每户生产的污水量等于该户自来水用量;②水费=自来水费用+污水处理费)
已知小王家2018年7月用水![]() 吨,交水费
吨,交水费![]() 元.8月份用水
元.8月份用水![]() 吨,交水费
吨,交水费![]() 元.
元.
(1)求![]() 的值;
的值;
(2)如果小王家9月份上交水费![]() 元,则小王家这个月用水多少吨?
元,则小王家这个月用水多少吨?
(3)小王家10月份忘记了去交水费,当他11月去交水费时发现两个月一共用水50吨,其中10月份用水超过![]() 吨,一共交水费
吨,一共交水费![]() 元,其中包含
元,其中包含![]() 元滞纳金,求小王家11月份用水多少吨? (滞纳金:因未能按期缴纳水费,逾期要缴纳的“罚款金额”)
元滞纳金,求小王家11月份用水多少吨? (滞纳金:因未能按期缴纳水费,逾期要缴纳的“罚款金额”)
参考答案:
【答案】(1)![]() ;(2)39;(3)11
;(2)39;(3)11
【解析】
(1)根据题意,列出关于a,b的二元一次方程组,即可求解;
(2)设小王家这个月用水![]() 吨(
吨(![]() ),根据小王家9月份上交水费
),根据小王家9月份上交水费![]() 元,列出方程,即可求解;
元,列出方程,即可求解;
(3)设小王家11月份用水![]() 吨,分两种情况,①当
吨,分两种情况,①当![]() 时,②当
时,②当![]() 时,分别列出方程,即可求解.
时,分别列出方程,即可求解.
![]() 由题意得:
由题意得: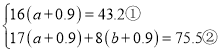
解①,得:![]() ,
,
将![]() 代入②,解得:
代入②,解得:![]() ,
,
![]() .
.
![]()
![]() ,
,
设小王家这个月用水![]() 吨(
吨(![]() ),由题意得:
),由题意得:
![]() ,
,
解得:![]() ,
,
经检验,![]() 是方程的解,且符合题意,
是方程的解,且符合题意,
答:小王家这个月用水![]() 吨.
吨.
![]() 设小王家11月份用水
设小王家11月份用水![]() 吨,
吨,
当![]() 时,
时,![]() ,
,
解得:![]() ;
;
当![]() 时,
时,![]()
解得![]() (舍去),
(舍去),
答:小王家11月份用水![]() 吨.
吨.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为( )

A.4,30° B.2,60° C.1,30° D.3,60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,对角线AC、BD相交于点O,E、F是AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
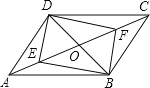
A.∠ADE=∠CBFB.∠ABE=∠CDFC.DE=BFD.OE=OF
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,AB=AD,对角线BD为⊙O的直径,AC与BD交于点E.点F为CD延长线上,且DF=BC.
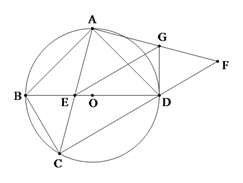
(1)证明:AC=AF;
(2)若AD=2,AF=
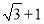 ,求AE的长;
,求AE的长;(3)若EG∥CF交AF于点G,连接DG.证明:DG为⊙O的切线.
-
科目: 来源: 题型:
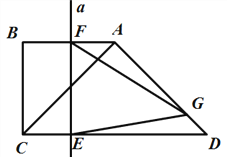
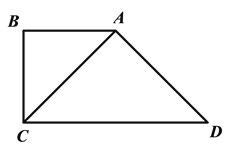
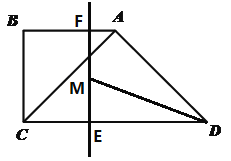
查看答案和解析>>【题目】两个等腰直角三角形如图放置,∠B=∠CAD=90°,AB=BC=
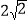 cm,AC=AD,垂直于CD的直线a从点C出发,以每秒
cm,AC=AD,垂直于CD的直线a从点C出发,以每秒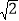 cm的速度沿CD方向匀速平移,与CD交于点E,与折线BAD交于点F;与此同时,点G从点D出发,以每秒1cm的速度沿着DA的方向运动;当点G落在直线a上,点G与直线a同时停止运动;设运动时间为t秒(t>0).
cm的速度沿CD方向匀速平移,与CD交于点E,与折线BAD交于点F;与此同时,点G从点D出发,以每秒1cm的速度沿着DA的方向运动;当点G落在直线a上,点G与直线a同时停止运动;设运动时间为t秒(t>0).(1)填空:CD=_______cm;
(2)连接EG、FG,设△EFG的面积为y,求y与t之间的函数关系式,并写出相应t的取值范围;
(3)是否存在某一时刻t(0<t<2),作∠ADC的平分线DM交EF于点M,是否存在点M是EF的中点?若存在,求此时的t值;若不存在,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】一副三角尺按照如图所示摆放在量角器上,边
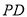 与量角器
与量角器 刻度线重合,边
刻度线重合,边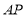 与量角器
与量角器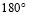 刻度线重合,将三角尺
刻度线重合,将三角尺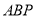 绕量角器中心点
绕量角器中心点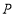 以每秒
以每秒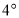 的速度顺时针旋转,当边
的速度顺时针旋转,当边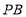 与
与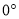 刻度线重合时停止运动.设三角尺
刻度线重合时停止运动.设三角尺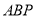 的运动时间为
的运动时间为 (秒)
(秒)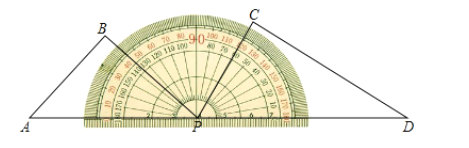
(1)当
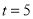 秒时,边
秒时,边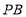 经过的量角器刻度线对应的度数为_ ;
经过的量角器刻度线对应的度数为_ ;(2)
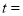 秒时,边
秒时,边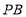 平分
平分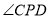 ;
;(3)若在三角尺
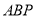 开始旋转的同时,三角尺
开始旋转的同时,三角尺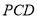 也绕点
也绕点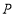 以每秒
以每秒 的速度逆时针旋转,当三角尺
的速度逆时针旋转,当三角尺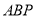 停止旋转时,三角尺
停止旋转时,三角尺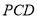 也停止旋转,
也停止旋转,①当
 为何值时,边
为何值时,边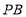 平分
平分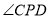 ;
;②在旋转过程中,是否存在某一时刻,使得 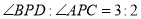 .若存在,请求出
.若存在,请求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标.

相关试题

