【题目】如图,四边形ABCD内接于⊙O,AB=AD,对角线BD为⊙O的直径,AC与BD交于点E.点F为CD延长线上,且DF=BC.
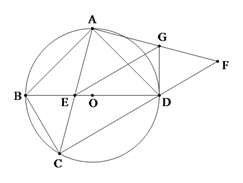
(1)证明:AC=AF;
(2)若AD=2,AF=![]() ,求AE的长;
,求AE的长;
(3)若EG∥CF交AF于点G,连接DG.证明:DG为⊙O的切线.
参考答案:
【答案】(1)证明见解析;
(2)AE的长为![]() ;
;
(3)证明见解析.
【解析】试题分析:(1)由圆的内接四边形的性质得:∠ABC+∠ADC=180°,又∠ADF+∠ADC=180°,故∠ABC=∠ADF,结合已知条件可证△ABC≌△ADF,从而可得结论;
(2)由(1)得AC=AF,由AB=AB得![]() ,得∠ADE=∠ACD.可证△ADE∽△ACD,得
,得∠ADE=∠ACD.可证△ADE∽△ACD,得![]() ,变换比例式从而得解;
,变换比例式从而得解;
(3)通过证明△ADG∽△AFD得∠ADG=∠F.再运用切线的判定定理即可得证.
试题解析:(1)证明:∵四边形ABCD内接于⊙O,∴∠ABC+∠ADC=180°.
∵∠ADF+∠ADC=180°,∴∠ABC=∠ADF.
在△ABC与△ADF中,
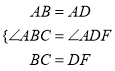 ,
,
∴△ABC≌△ADF.
∴AC=AF;
(2)由(1)得,AC=AF=![]() .
.
∵AB=AD,
∴![]()
∴∠ADE=∠ACD.
∵∠DAE=∠CAD,
∴△ADE∽△ACD.
∴![]() .
.
∴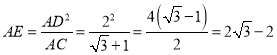 .
.
(3)证明:∵EG∥CF,∴ ![]() .
.
∴AG=AE.
由(2)得![]() ,∴
,∴![]() .
.
∵∠DAG=∠FAD,∴△ADG∽△AFD.
∴∠ADG=∠F.
∵AC=AF,∴∠ACD=∠F.
又∵∠ACD=∠ABD,
∴∠ADG=∠ABD.
∵BD为⊙O的直径,
∴∠BAD=90°.
∴∠ABD+∠BDA=90°.∴∠ADG+∠BDA=90°.
∴GD⊥BD.
∴DG为⊙O的切线.
-
科目: 来源: 题型:
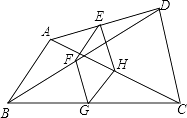
查看答案和解析>>【题目】如图,点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,当四边形ABCD的边至少满足条件时,四边形EFGH是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为 .
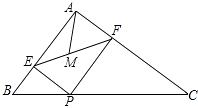
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD和菱形ECGF的边长分别为4和6,∠A=120°,则阴影部分的面积是 .
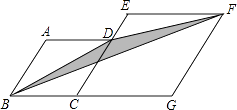
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣2x2y3)2(xy)3
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:x2﹣6x+8=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若2x+5y﹣3=0,求4x32y的值.
相关试题

