【题目】已知:如图,C是AB上一点,点D,E分别在AB两侧,AD∥BE,且AD=BC,BE=AC. 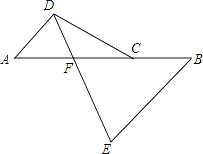
(1)求证:CD=CE;
(2)连接DE,交AB于点F,猜想△BEF的形状,并给予证明.
参考答案:
【答案】
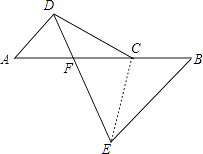
(1)证明:如图,连接CE,
∵AD∥BE,
∴∠A=∠B,
在△ADC和△BCE中
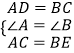
∴△ADC≌△BCE(SAS),
∴CD=CE
(2)解:△BEF为等腰三角形,证明如下:
由(1)可知CD=CE,
∴∠CDE=∠CED,
由(1)可知△ADC≌△BEC,
∴∠ACD=∠BEC,
∴∠CDE+∠ACD=∠CED+∠BEC,
即∠BFE=∠BED,
∴BE=BF,
∴△BEF是等腰三角形.
【解析】(1)连接CE,由平行线的性质,结合条件可证明△ADC≌△BCE,可证明CD=CE;(2)由(1)中的全等可得∠CDE=∠CED,∠ACD=∠BEC,可证明∠BFE=∠BEF,可证明△BEF为等腰三角形.
【考点精析】本题主要考查了平行线的性质的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】超市店庆促销,某种书包原价每个x元,第一次降价打“八折”,第二次降价每个又减10元,经两次降价后售价为90元,则得到方程( )
A.0.8x﹣10=90
B.0.08x﹣10=90
C.90﹣0.8x=10
D.x﹣0.8x﹣10=90 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列数值中,是不等式x-2>2的一个解的是( )
A. 0 B. 2
C. 4 D. 6
-
科目: 来源: 题型:
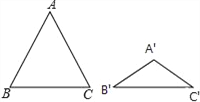
查看答案和解析>>【题目】如图,△ABC与△A′ B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为 _______。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:64x2=49,(y﹣2)3+1=0,求x+y=
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(x+3)(2x-1)是多项式__________因式分解的结果.
相关试题

