【题目】已知:如图,抛物线y=﹣ ![]() (x﹣h)2+k与x轴交于A、B,与y轴交于C,抛物线的顶点为D,对称轴交x轴于H,直线y=
(x﹣h)2+k与x轴交于A、B,与y轴交于C,抛物线的顶点为D,对称轴交x轴于H,直线y= ![]() x+
x+ ![]() 经过点A与对称轴交于E,点E的纵坐标为3.
经过点A与对称轴交于E,点E的纵坐标为3.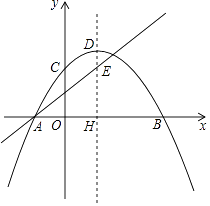
(1)求h、k的值;
(2)点P为第四象限抛物线上一点,连接PH,点Q为PH的中点,连接AQ、AP,设点P的横坐标为t,△AQP的面积为S,求S与t的函数关系式(直接写出自变量t的取值范围);
(3)在(2)的条件下,过点Q作y轴的平行线QK,过点D作y轴的垂直DK,直线QK、DK交于点K,连接PK、EK,若2∠DKE+∠HPK=90°,求点P的横坐标.
参考答案:
【答案】
(1)解:∵点E的纵坐标为3,
∴3= ![]() x+
x+ ![]() ,
,
解得:x=2,
∴D点的横坐标是2,
∴h=2,
∵直线y= ![]() x+
x+ ![]() 经过点A,
经过点A,
∴A(﹣2,0)代入y=﹣ ![]() (x﹣h)2+k得,0=﹣
(x﹣h)2+k得,0=﹣ ![]() (﹣2﹣h)2+k,
(﹣2﹣h)2+k,
∴k=4;
(2)解:如图1,设P的横坐标为t,则纵坐标为﹣ ![]() t2+t+3,
t2+t+3,
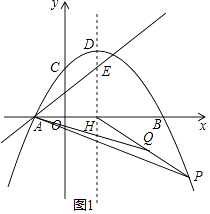
∵点Q为PH的中点,
∴S△APQ=S△AQH,
∴S△APQ= ![]() S△AHP,
S△AHP,
∵S△AHP= ![]() AH(
AH( ![]() t2﹣t﹣3),
t2﹣t﹣3),
∵AH=4,
∴S= ![]() ×4×((
×4×(( ![]() t2﹣t﹣3)=
t2﹣t﹣3)= ![]() t2﹣t﹣3(t>6);
t2﹣t﹣3(t>6);
(3)解:如图2,过P作x轴、y轴的平行线分别交DH,KQ于M,N,交直线DK于R,
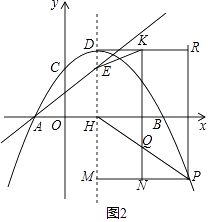
则四边形DKNM,四边形KNPR是矩形,
设MN=m,
∴DK=KR=m,
∴P点的横坐标为2m+2,代入y=﹣ ![]() (x﹣2)2+4中,
(x﹣2)2+4中,
得到P点的纵坐标为:﹣m2+4,∴DM=RP=m2,
∴tan∠DKE= ![]() =
= ![]() ,
,
∴∠DKE=∠KPR,
∴EK⊥PK,
∵2∠DKE+∠HPK=90°,∠DKE=∠KPR,∠BHP+∠HPK+∠KPR=90°,
∴∠DKE=∠PHB,
∴tan∠DKE=tan∠PHB,
∴ ![]() =
= ![]() ,
,
∴m=± ![]() (m=﹣
(m=﹣ ![]() 舍去),
舍去),
∴m= ![]() ,
,
∴点P的横坐标为2+2 ![]() .
.
【解析】(1)先求出E的横坐标,等于D的横坐标,即h值,再把A坐标代入抛物线解析式求出k;(2)由“Q为PH的中点”可知△APQ与△AHP是同高等底三角形,面积相等,因此可用t的代数式表示S△AHP,再乘以![]() ;(3)由"2∠DKE+∠HPK=90°"可推出∠DKE=∠KPR,∠BHP+∠HPK+∠KPR=90°,∠DKE=∠KPR,根据二者的正切定义构建等式,求出m.
;(3)由"2∠DKE+∠HPK=90°"可推出∠DKE=∠KPR,∠BHP+∠HPK+∠KPR=90°,∠DKE=∠KPR,根据二者的正切定义构建等式,求出m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.

(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;②当AM的值为 时,四边形AMDN是菱形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC=( )
A. 35° B. 45° C. 50° D. 55°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的面积为16,BC=8.现将△ABC沿直线BC向右平移a个单位到△DEF的位置.
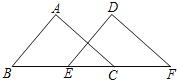
(1)当△ABC所扫过的面积为32时,求a的值;
(2)连接AE、AD,当AB=5,a=5时,试判断△ADE的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“父母恩深重,恩怜无歇时”,每年5月的第二个星期日即为母亲节,节日前夕巴蜀中学学生会计划采购一批鲜花礼盒赠送给妈妈们.
(1)经过和花店卖家议价,可在原标价的基础上打八折购进,若在花店购买80个礼盒最多花费7680元,请求出每个礼盒在花店的最高标价;(用不等式解答)
(2)后来学生会了解到通过“大众点评”或“美团”同城配送会在(1)中花店最高售价的基础上降价25%,学生会计划在这两个网站上分别购买相同数量的礼盒,但实际购买过程中,“大众点评”网上的购买价格比原有价格上涨 m%,购买数量和原计划一样:“美团”网上的购买价格比原有价格下降了
m%,购买数量和原计划一样:“美团”网上的购买价格比原有价格下降了 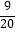 m元,购买数量在原计划基础上增加15m%,最终,在两个网站的实际消费总额比原计划的预算总额增加了
m元,购买数量在原计划基础上增加15m%,最终,在两个网站的实际消费总额比原计划的预算总额增加了 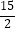 m%,求出m的值.
m%,求出m的值. -
科目: 来源: 题型:
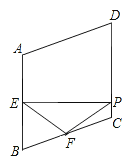
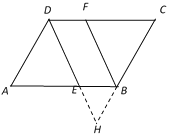
查看答案和解析>>【题目】如图,直线AD∥BC,E,F分别在线段AB,CD上,∠ADE=∠FBC,判断直线DE与BF的位置关系,以下是解答过程,请补充完整,其中括号里填依据.
解:DE∥BF.
理由如下:延长DE交CB延长线于H点,
因为AD∥BC(__________).
所以∠ADE=∠H(__________).
又因为∠ADE=∠FBC(已知),
所以______=______(________).
所以DE∥BF(___________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=90°,AH⊥BC于点H,过点C作CD⊥AC,连接AD,点M为AC上一点,且AM=CD,连接BM交AH于点N,交AD于点E.
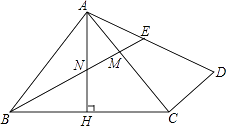
(1)若AB=3,AD=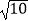 ,求△BMC的面积;
,求△BMC的面积;
(2)点E为AD的中点时,求证:AD=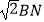 .
.
相关试题

