【题目】盒子里装有红球和白球共10个,它们除颜色外其他都相同,每次从盒子里摸出1个球,记下颜色后放回盒子里摇匀再摸.在摸球活动中得到下列表中部分数据.
摸球次数 | 出现红球的频数 | 出现红球的频率 | 摸球次数 | 出现红球的频数 | 出现红球的频率 |
50 | 17 | 34% | 350 | 103 | 29.4% |
100 | 32 | 32% | 400 | 123 | |
150 | 44 | 29.3% | 450 | 136 | 30.2% |
200 | 64 | 32% | 500 | 148 | 29.6% |
250 | 78 | 31.2% | 550 | 167 | |
300 | 32% | 600 | 181 | 30.2% |
(1)请将表中数据补充完整.
(2)画出出现红球的频率的折线统计图.
(3)观察所画折线统计图,你发现了什么?
(4)你认为盒子里哪种颜色的球多?
(5)如果从盒子里任意摸出一球,你认为摸到白球的概率有多大?
参考答案:
【答案】(1) 96;30.8%;30.4%;(2)详见解析;(3)观察折线统计图可以发现:随着摸球次数的增多,出现红球的频率在30%上下浮动.(4)由(3)可以估计盒子里白球的个数比红球多.(5)70%.
【解析】试题分析:(1)利用频数=频率×摸球次数计算数据即可;
(2)根据表格提供的数据作出条形统计图即可;
(3)通过观察统计图找到其频率逐渐稳定到哪个常数附近即可;
(4)根据频率的大小进行比较即可;
(5)用1减去摸到红球的概率就是摸到白球的概率.
试题解析:(1)表中依次填为:96;30.8%;30.4%从左往右,从上往下.
(2)如图:
 .
.
(3)观察折线统计图可以发现:随着摸球次数的增多,出现红球的频率在30%上下浮动.
(4)由(3)可以估计盒子里白球的个数比红球多.
(5)如果从盒子里任意摸出一球,摸到白球的概率是
1-30%=70%.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线MN与直线PQ垂直相交于O,点A在射线OP上运动,点B 在射线OM上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,AD、BC的延长线交于点F,点A、B在运动的过程中,∠F= °;DE、CE又分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小也不发生变化,其大小为∠CED= °.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其延长线相交于E、F,则∠EAF= ° ;在△AEF中,如果有一个角是另一个角的3倍,则∠ABO= °.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD,OP是∠BOC的平分线.
(1)请写出图中所有∠EOC的补角 ____________________;
(2)如果∠POC:∠EOC=2:5.求∠BOF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学举行“中国梦校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和告知给你代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
(1)根据图示填写表格;
平均数/分
中位数/分
众数/分
初中代表队
高中代表队
(2)计算两队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.

-
科目: 来源: 题型:
查看答案和解析>>【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,由于该十字路口右拐弯处是通往新建经济开发区的,因此交管部门在汽车行驶高峰时段对车流量作了统计,发现汽车在此十字路口向右转的频率为
 ,向左转和直行的频率均为
,向左转和直行的频率均为 .
.(1)假设平均每天通过该路口的汽车为5 000辆,求汽车在此向左转、向右转、直行的车辆各是多少辆;
(2)目前在此路口,汽车向左转、向右转、直行的绿灯亮的时间都为30 s,在绿灯亮总时间不变的条件下,为了缓解交通拥挤,请你利用概率的知识对此路口三个方向的绿灯亮的时间做出合理的调整.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了预测本校应届毕业女生“一分钟跳绳”项目考试情况,从九年级随机抽取部分女生进行该项目测试,并以测试数据为样本,绘制出如图10所示的部分频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值)和扇形统计图.根据统计图提供的信息解答下列问题:
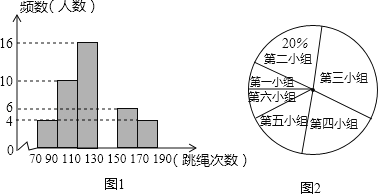
(1)补全频数分布直方图,并指出这个样本数据的中位数落在第 小组;
(2)若测试九年级女生“一分钟跳绳”次数不低于130次的成绩为优秀,本校九年级女生共有260人,请估计该校九年级女生“一分钟跳绳”成绩为优秀的人数;
(3)如测试九年级女生“一分钟跳绳”次数不低于170次的成绩为满分,在这个样本中,从成绩为优秀的女生中任选一人,她的成绩为满分的概率是多少?
-
科目: 来源: 题型:
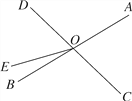
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.
(1)图中∠AOC的对顶角为________,∠BOE的补角为________;
(2)若∠AOC=75°,且∠BOE∶∠EOD=1∶4,求∠AOE的度数.
相关试题

