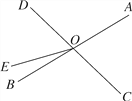
【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.
(1)图中∠AOC的对顶角为________,∠BOE的补角为________;
(2)若∠AOC=75°,且∠BOE∶∠EOD=1∶4,求∠AOE的度数.
参考答案:
【答案】 ∠BOD ∠AOE
【解析】试题分析:(1)利用对顶角、邻补角的定义直接回答即可;
(2)根据对顶角相等求出∠BOD的度数,再根据∠BOE:∠EOD=1:4求出∠BOE的度数,然后利用互为邻补角的两个角的和等于180°即可求出∠AOE的度数.
试题解析:
解:(1)∠BOD ∠AOE
(2)∵∠DOB=∠AOC=75°,∠DOB=∠BOE+∠EOD,
∠BOE∶∠EOD=1∶4,
∴∠EOD=4∠BOE,
∴∠BOE+4∠BOE=75°,
∴∠BOE=15°,
∴∠AOE=180°-∠BOE=165°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】盒子里装有红球和白球共10个,它们除颜色外其他都相同,每次从盒子里摸出1个球,记下颜色后放回盒子里摇匀再摸.在摸球活动中得到下列表中部分数据.
摸球次数
出现红球的频数
出现红球的频率
摸球次数
出现红球的频数
出现红球的频率
50
17
34%
350
103
29.4%
100
32
32%
400
123
150
44
29.3%
450
136
30.2%
200
64
32%
500
148
29.6%
250
78
31.2%
550
167
300
32%
600
181
30.2%
(1)请将表中数据补充完整.
(2)画出出现红球的频率的折线统计图.
(3)观察所画折线统计图,你发现了什么?
(4)你认为盒子里哪种颜色的球多?
(5)如果从盒子里任意摸出一球,你认为摸到白球的概率有多大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,由于该十字路口右拐弯处是通往新建经济开发区的,因此交管部门在汽车行驶高峰时段对车流量作了统计,发现汽车在此十字路口向右转的频率为
 ,向左转和直行的频率均为
,向左转和直行的频率均为 .
.(1)假设平均每天通过该路口的汽车为5 000辆,求汽车在此向左转、向右转、直行的车辆各是多少辆;
(2)目前在此路口,汽车向左转、向右转、直行的绿灯亮的时间都为30 s,在绿灯亮总时间不变的条件下,为了缓解交通拥挤,请你利用概率的知识对此路口三个方向的绿灯亮的时间做出合理的调整.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了预测本校应届毕业女生“一分钟跳绳”项目考试情况,从九年级随机抽取部分女生进行该项目测试,并以测试数据为样本,绘制出如图10所示的部分频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值)和扇形统计图.根据统计图提供的信息解答下列问题:
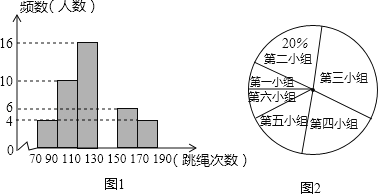
(1)补全频数分布直方图,并指出这个样本数据的中位数落在第 小组;
(2)若测试九年级女生“一分钟跳绳”次数不低于130次的成绩为优秀,本校九年级女生共有260人,请估计该校九年级女生“一分钟跳绳”成绩为优秀的人数;
(3)如测试九年级女生“一分钟跳绳”次数不低于170次的成绩为满分,在这个样本中,从成绩为优秀的女生中任选一人,她的成绩为满分的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“爆竹声声一岁除”,除夕和春节期间燃放爆竹是中国人的传统风俗习惯,但这种习惯会造成空气污染,为了了解某市市民春节期间购买、燃放烟花爆竹的原因,该市统计局随机调查了该市部分15周岁以上常住市民,对调查结果整理后,绘制如图尚不完整的统计图表.
组别
原因
人数
A
不想改变传统风俗习惯
650
B
增添节日喜庆气氛
300
C
祈福运、求吉利、辟邪害
m
D
没有可替代的庆祝方式
150
E
为了孩子的玩耍和快乐
n
F
其他
100
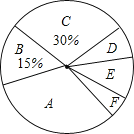
请根据图表中提供的信息解答下列问题:
(1)填空:m= ,n= ,扇形统计图中D组所占的百分比为 .
(2)若该市人口约为800万,请你估计其中属于B组的市民有多少人?(用科学记数法表示);
(3)若在此次接受调查的市民中随机抽取一人,此人属于A组的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司计划2016年在甲、乙两个电视台播放总时长为300分钟的广告,已知甲、乙两电视台的广告收费标准分别为500元/分钟和200元/分钟,该公司的广告总费用为9万元.预计甲、乙两个电视台播放该公司的广告能给该公司分别带来0.3万元/分钟和0.2万元/分钟的收益,该公司在甲、乙两个电视台播放广告的时长应分别为多少分钟?预计甲、乙两电视台2016年为此公司所播放的广告将给该公司带来多少万元的总收益?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
(1)求证:△MBA≌△NDC;
(2)四边形MPNQ是什么样的特殊四边形?请说明理由.

相关试题

