【题目】如图所示,在平面直角坐标系中,过点A(﹣ ![]() ,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根
,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根
(1)求线段BC的长度;
(2)试问:直线AC与直线AB是否垂直?请说明理由;
(3)若点D在直线AC上,且DB=DC,求直线BD的解析式;
(4)在x轴上是否存在P,使以O、B、P三点为顶点的三角形与△ABC相似?若存在,请直接写出P点的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:∵由x2﹣2x﹣3=0得:
∴x1=3,x2=﹣1
∴B(0,3),C(0,﹣1),
∴BC=4.
(2)
解:结论:AC⊥AB.理由如下:
∵A( ![]() ,0),B(0,3),C(0,﹣1),
,0),B(0,3),C(0,﹣1),
∴OA= ![]() ,OB=3,OC=1,
,OB=3,OC=1,
∴tan∠ABO= ![]() =
= ![]() ,tan∠ACO=
,tan∠ACO= ![]() =
= ![]() ,
,
∴∠ABO=30°,∠ACO=60°,
∴∠BAC=90°,
∴AC⊥AB
(3)
解:如图1中,过D作DE⊥x轴于E.
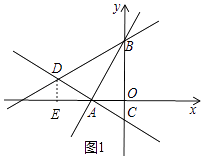
∴∠DEA=∠AOC=90°,
∵tan∠ACO= ![]() =
= ![]() ,
,
∵∠DCB=60°
∵DB=DC,
∴△DBC是等边三角形,
∵BA⊥DC,
∴DA=AC,
∵∠DAE=∠OAC,
∴△ADE≌△ACO,
∴DE=OC=1,AE=OA= ![]()
∴ ![]() ,
,
∴D的坐标为( ![]() ,1).
,1).
设直线BD的解析式为y=kx+b,则有 ![]() 解得
解得 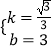 ,
,
∴直线BD的解析式为y= ![]() x+3
x+3
(4)
解:存在.如图2中,延长BD交x轴于P1.
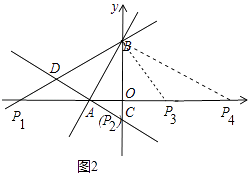
由(3)可知,△DBC是等边三角形,
∴∠P1BO=60°,
∵在△ABC中,∠ACB=60°,∠CAB=90°,
∴∠P1BC=∠ACB=60°,∵∠P1OB=∠CAB=90°,
∴△P1BO∽△BCA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴OP1=3 ![]() ,
,
∴P1(﹣3 ![]() ,0),
,0),
当P2与A重合时,△BOP2∽△BAC,此时P2(﹣ ![]() ,0),
,0),
再根据对称性可得P3( ![]() ,0),P4(3
,0),P4(3 ![]() ,0)也符合条件.
,0)也符合条件.
综上所述,点P的坐标为(﹣3 ![]() ,0)或(﹣
,0)或(﹣ ![]() ,0)或(
,0)或( ![]() ,0)或(3
,0)或(3 ![]() ,0)
,0)
【解析】(1)列方程即可求出点B、C坐标解决问题.(2)由tan∠ABO= ![]() =
= ![]() ,tan∠ACO=
,tan∠ACO= ![]() =
= ![]() ,推出∠ABO=30°,∠ACO=60°,即可解决问题.(3)如图1中,过D作DE⊥x轴于E.由△ADE≌△ACO,推出DE=OC=1,AE=OA=
,推出∠ABO=30°,∠ACO=60°,即可解决问题.(3)如图1中,过D作DE⊥x轴于E.由△ADE≌△ACO,推出DE=OC=1,AE=OA= ![]() ,求出点D坐标,利用待定系数法即可解决问题.(4)存在.如图2中,延长BD交x轴于P1 . 可以证明P1满足条件,当P2与A重合时也满足条件,再根据对称性写出P3、P4坐标即可.
,求出点D坐标,利用待定系数法即可解决问题.(4)存在.如图2中,延长BD交x轴于P1 . 可以证明P1满足条件,当P2与A重合时也满足条件,再根据对称性写出P3、P4坐标即可.
【考点精析】解答此题的关键在于理解一次函数的性质的相关知识,掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小,以及对一次函数的图象和性质的理解,了解一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
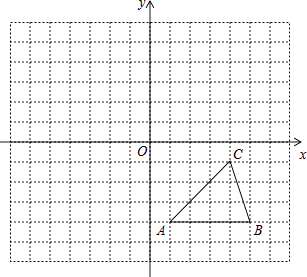
(1)把△ABC向上平移5个单位后得到对应的△A1B1C1 , 画出△A1B1C1 , 并写出C1的坐标.
(2)以点B为位似中心在格纸内画出△A2BC2 , 且与△ABC的位似比为2:1,并写出C2的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在四边形ABCD中,AD∥BC,∠C=90°,AB=AD=50,BC=64,连结BD,AE⊥BD垂足为E,

(1)求证:△ABE∽△DCB;
(2)求线段DC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,先把一矩形ABCD纸片上下对折,设折痕为MN;如图②,再把点B 叠在折痕线MN上,得到Rt△ABE.过B点作PQ⊥AD,分别交BC、AD于点P、Q.
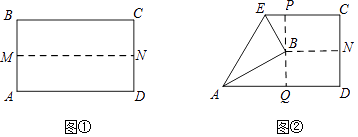
(1)求证:△PBE∽△QAB;
(2)在图②中,EB是否平分∠AEC?请说明理由;
(3)在(1)(2)的条件下,若AB=4,求PE的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】(14分) 已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于CE,垂足为H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )

A.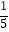
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】威远人民商场准备购进甲、乙两种牛奶进行销售,若甲种牛奶的进价比乙种牛奶的进价每件少5元,其用90元购进甲种牛奶的数量与用100元购进乙种牛奶的数量相同.
(1)求甲种牛奶、乙种牛奶的进价分别是多少元?
(2)若该商场购进甲种牛奶的数量是乙种牛奶的3倍少5件,两种牛奶的总数不超过95件,该商场甲种牛奶的销售价格为49元,乙种牛奶的销售价格为每件55元,则购进的甲、乙两种牛奶全部售出后,可使销售的总利润(利润=售价﹣进价)超过371元,请通过计算求出该商场购进甲、乙两种牛奶有哪几种方案?
相关试题

