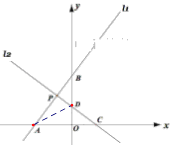
【题目】如图,直线![]() 的解析式为y=
的解析式为y=![]() x+4,与x轴y轴分别交于A,B两点;直线
x+4,与x轴y轴分别交于A,B两点;直线![]() 与x轴交于点C(2,0)与y轴交于点D(0,
与x轴交于点C(2,0)与y轴交于点D(0, ![]() ),两直线交于点P.
),两直线交于点P.
(1)求点A,B的坐标及直线![]() 的解析式;
的解析式;
(2)求证:△AOB≌△APC;
(3)若将直线![]() 向右平移m个单位,与x轴,y轴分别交于点
向右平移m个单位,与x轴,y轴分别交于点![]() 、
、![]() ,使得以点A、B、
,使得以点A、B、![]() 、
、![]() 为顶点的图形是轴对称图形,求m的值?
为顶点的图形是轴对称图形,求m的值?

参考答案:
【答案】(1)A(-3,0),B(0,4),l2: ![]() ;(2)证明见解析;(3)m=1.
;(2)证明见解析;(3)m=1.
【解析】试题分析:(1)根据直线![]() 的解析式为y=
的解析式为y=![]() x+4,分别令x=0、y=0即可得出A、B坐标,直线
x+4,分别令x=0、y=0即可得出A、B坐标,直线![]() 利用待定系数法即可求得;
利用待定系数法即可求得;
(2)连接AD,先证明△ADB≌△ADC,得到∠ABO=∠ACP,再根据ASA证明△AOB≌△APC即可;
(3)由B、D′都在y轴上,A、C′在x轴上,可知要想使得以点A、B、C′、D′为顶点的图形是轴对称图形,必有A、C′关于y轴对称,从而得解.
试题解析:(1)当x=0时,y=![]() x+4=4,当y=0时,0=
x+4=4,当y=0时,0=![]() x+4,解得:x=-3,
x+4,解得:x=-3,
∴A(-3,0),B(0,4),
设直线![]() 的解析式为:y=kx+b,由题意得:
的解析式为:y=kx+b,由题意得: 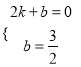 ,解得:
,解得: 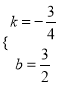 ,
,
∴直线![]() :y=
:y=![]() ;
;
(2)连接AD,
由B(0,4),D(0, ![]() ),A(-3,0),C(2,0)可得:BD=
),A(-3,0),C(2,0)可得:BD=![]() ,AC=AB=5,
,AC=AB=5,
又由OC=2,OD=![]() 得CD=
得CD=![]() =
=![]() =BD,
=BD,
在△ADB和△ADC中 ,∴△ADB≌△ADC,∴∠ABO=∠ACP,
,∴△ADB≌△ADC,∴∠ABO=∠ACP,
在△AOB和△APC中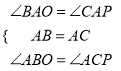 ,∴△AOB≌△APC;
,∴△AOB≌△APC;
(3)∵B、D′都在y轴上,A、C′在x轴上,
∴要想使得以点A、B、C′、D′为顶点的图形是轴对称图形,必有A、C′关于y轴对称,
∴C′(3,0),
∵C(2,0),
∴m=3-2=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若9x2﹣3(m﹣5)x+16是完全平方式,则m=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x2+4x+8y+y2+20=0,则x﹣y=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,BE平分∠ABC交AD于点E,F为BE上一点,连接DF,过F作FG⊥DF交BC于点G,连接BD交FG于点H,若FD = FG,
 ,BG = 4,则GH的长为__________.
,BG = 4,则GH的长为__________.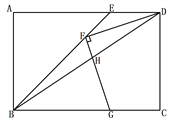
-
科目: 来源: 题型:
查看答案和解析>>【题目】嘉兴市某天的最高气温为 8℃,最低气温为 -1℃,则这天嘉兴的最高气温与最低气温差为( )
A.7℃B.8℃C.9℃D.10℃
-
科目: 来源: 题型:
查看答案和解析>>【题目】节约用水是我们的美德,水龙头关闭不严会造成滴水,容器内盛水
 与滴水时间
与滴水时间 的关系用可以显示水量的容器做如图
的关系用可以显示水量的容器做如图 的试验,并根据试验数据绘制出如图
的试验,并根据试验数据绘制出如图 的函数图象,结合图象解答下列问题.
的函数图象,结合图象解答下列问题.(
 )容器内原有水多少升.
)容器内原有水多少升.(
 )求
)求 与
与 之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升.
之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,对角线AC、BD交于点O,点E是BC上一点,且AB=BE,∠1=15°,则∠2=________°.

相关试题

