【题目】如图,已知⊙O的直径AB垂直于弦CD于点E,过C点作CG∥AD交AB的延长线于点G,连接CO并延长交AD于点F,且CF⊥AD.
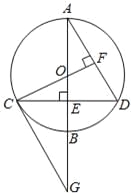
(1)试问:CG是⊙O的切线吗?说明理由;
(2)请证明:E是OB的中点;
(3)若AB=8,求CD的长.
参考答案:
【答案】(1) CG是⊙O的切线,理由见解析;(2)证明见解析;(3)![]() .
.
【解析】试题分析:(1)已知点C在圆上,根据平行线的性质可得∠FCG=90°,即OC⊥CG;故CG是⊙O的切线.
(2)方法比较多,应通过等边三角形的性质或三角形全等的思路来考虑;
(3)Rt△OCE中,有三角函数的定义,可得CE=OE×cot30°,故代入OE=2可得CE的长.
试题解析:(1)CG是⊙O的切线.
理由如下:
∵CG∥AD,
∵CF⊥AD,
∴OC⊥CG.
∴CG是⊙O的切线;
(2)第一种方法:连接AC,如图,
∵CF⊥AD,AE⊥CD且CF,AE过圆心O,
∴![]() .
.
∴AC=AD=CD.
∴△ACD是等边三角形.
在Rt△COE中,
∴OE=![]() OB.
OB.
∴点E为OB的中点.
![]() .
.
∵AE⊥CD,且AE过圆心O,
∴CE=DE.
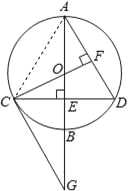
(3)∵AB=8,
∴OC=![]() AB=4.
AB=4.
又∵BE=OE,
∴OE=2.
∴CE=OE×cot30°=![]() .
.
∵AB⊥CD,
∴CD=2CE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着电子技术的不断进步,电子元件的尺寸大幅度缩小,在芯片上某种电子元件大约只占0.00000065m2.这个数用科学记数法表示为_____m2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a+b=3,ab=2,求代数式a3b+2a2b2+ab3的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】x取___时,式子(x+3)2+15的值最小,这个最小值是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
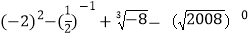 ; (2)
; (2) 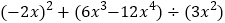 ;
;(3)
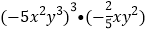 ; (4)
; (4)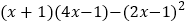 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.

(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系中,△ABC的位置如图所示.
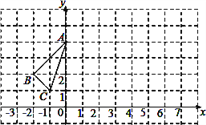
(1)请写出A、B、C三点的坐标;
(2)请求出△ABC的面积;
(3)将△ABC向右平移6个单位,再向上平移2个单位,请在图中作出平移后的△A′B′C′.
相关试题

