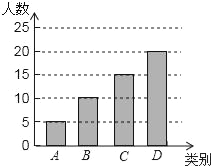
【题目】某市有三个景区是人们节假日游玩的热点景区,某学校对七(1)班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别,A:三个景区;B:游两个景区;C:游一个景区;D:不到这三个景区游玩,现根据调查结果绘制了如下不完全的条形统计图和扇形统计图,请结合图中信息解答下列问题:
(1)九(1)班现有学生__________人,在扇形统计图中表示“B类别”的扇形的圆心角的度数为__________;
(2)请将条形统计图补充完整;
(3)若该校七年级有1000名学生,求计划“五一”小长假随父母到这三个景区游玩的学生多少名?

参考答案:
【答案】(1)50;72°;(2)补图见解析;(3)计划“五一”小长假随父母到这三个景区游玩的学生人数是600人.
【解析】试题分析:(1)根据图象得到信息.(2)先算出总人数,再分别计算度数,补充统计图.
(3)用总人数乘以去三个景区的百分比.
试题解析:
解:(1)∵A类5人,占10%,
∴八(1)班共有学生有:5÷10%=50(人);
∴在扇形统计图中,表示“B类别”的扇形的圆心角的度数为: ![]() ×360°=72°;
×360°=72°;
故答案为:50,72°.
(2)D类:50﹣5﹣10﹣15=20(人),如图:
 ;
;
(3)计划“五一”小长假随父母到这三个景区游玩的学生人数是1000×(1﹣![]() )=600(人).
)=600(人).
答:计划“五一”小长假随父母到这三个景区游玩的学生人数是600人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】按照题中提供的思路点拨,先填空,然后完成解答的全过程.
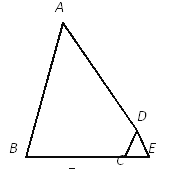
如图,已知AB=AD,∠BAD=60°,∠BCD=120°,延长BC,使CE=CD,连接DE,求证:BC+DC=AC.
思路点拨:(1)由已知条件AB=AD,∠BAD=60°,可知△ABD是_三角形.同理由已知条件∠BCD=120°得到∠DCE=_,且CE=CD,可知_;
(2)要证BC+DC=AC,可将问题转化为证两条线段相等,即_=_;
(3)要证(2)中所填写的两条线段相等,可以先证明_.请写出完整的证明过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为保护环境,我市公交公司计划购买A型和B型两种环保节能公交车共10辆.若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?
(3)在(2)的条件下,哪种购车方案总费用最少?最少总费用是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程3x+1=m+4的解是x=2,则m值是( )
A.2B.5C.3D.1
-
科目: 来源: 题型:
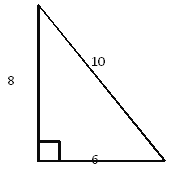
查看答案和解析>>【题目】如图,已知一个边长分别为6、8、10的直角三角形,请设计出一个有一条边长为8的直角三角形,使这两个直角三角形能够拼成一个等腰三角形.
(1)画出4种不同拼法(周长不等)的等腰三角形;
(2)分别求出4种不同拼法的等腰三角形的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当x=﹣2时,下列不等式成立的是( )
A.x﹣5>﹣7B.x﹣2<0C.2(x﹣2)>﹣2D.3x>2x
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A.两条直线被第三条直线所截,同位角相等
B.在同一平面内,垂直于同一条直线上的两直线平行
C.在同一平面内,平行于同一直线的两直线平行
D.两点之间线段最短
相关试题

