【题目】如图,已知点A是第一象限内横坐标为2 ![]() 的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是 .
的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是 . 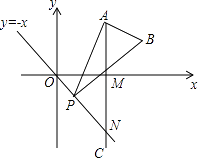
参考答案:
【答案】2 ![]()
【解析】解:由题意可知,OM=2 ![]() ,点N在直线y=﹣x上,AC⊥x轴于点M,则△OMN为等腰直角三角形,ON=
,点N在直线y=﹣x上,AC⊥x轴于点M,则△OMN为等腰直角三角形,ON= ![]() OM=
OM= ![]() ×2
×2 ![]() =
= ![]() .
.
如答图①所示,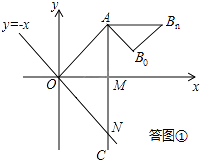
设动点P在O点(起点)时,点B的位置为B0 , 动点P在N点(终点)时,点B的位置为Bn , 连接B0Bn
∵AO⊥AB0 , AN⊥ABn , ∴∠OAC=∠B0ABn ,
又∵AB0=AOtan30°,ABn=ANtan30°,∴AB0:AO=ABn:AN=tan30°(此处也可用30°角的Rt△三边长的关系来求得),
∴△AB0Bn∽△AON,且相似比为tan30°,
∴B0Bn=ONtan30°= ![]() ×
× ![]() =2
=2 ![]() .
.
现在来证明线段B0Bn就是点B运动的路径(或轨迹).
如答图②所示,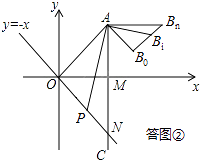
当点P运动至ON上的任一点时,设其对应的点B为Bi , 连接AP,ABi , B0Bi
∵AO⊥AB0 , AP⊥ABi , ∴∠OAP=∠B0ABi ,
又∵AB0=AOtan30°,ABi=APtan30°,∴AB0:AO=ABi:AP,
∴△AB0Bi∽△AOP,∴∠AB0Bi=∠AOP.
又∵△AB0Bn∽△AON,∴∠AB0Bn=∠AOP,
∴∠AB0Bi=∠AB0Bn ,
∴点Bi在线段B0Bn上,即线段B0Bn就是点B运动的路径(或轨迹).
综上所述,点B运动的路径(或轨迹)是线段B0Bn , 其长度为 ![]() .
.
所以答案是: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小苏和小林在如图所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如下图所示.下列叙述正确的是( )

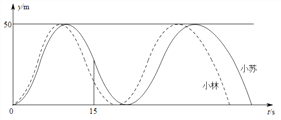
A. 两人从起跑线同时出发,同时到达终点
B. 小苏跑全程的平均速度大于小林跑全程的平均速度
C. 小苏前15s跑过的路程大于小林前15s跑过的路程
D. 小林在跑最后100m的过程中,与小苏相遇2次
-
科目: 来源: 题型:
查看答案和解析>>【题目】一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图方式进行拼接.
(1)若把4张、8张这样的餐桌拼接起来,四周分别可坐多少人?
(2)若用餐的人数有90人,则这样的餐桌需要多少张? -
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小龙沿着一条笔直的马路进行长跑比赛,小明在比赛过程中始终领先小龙,并匀速跑完了全程,小龙匀速跑了几分钟后提速和小明保持速度一致,又过了1分钟,小龙因体力问题,不得已又减速,并一直以这一速度完成了余下的比赛, 完成比赛所用时间比小明多了1分钟,已知小明跑后4分20秒时领先小龙175米,小明与小龙之间的距离
 (米)与他们所用时间
(米)与他们所用时间 (分钟)之间的函数关系如图所示.有下列说法:①小明到达终点时,小龙距离终点还有225米;②小明的速度是300米/分;③小龙提速前的速度是200米/分;④比赛全程为1 500米.其中正确的是( )
(分钟)之间的函数关系如图所示.有下列说法:①小明到达终点时,小龙距离终点还有225米;②小明的速度是300米/分;③小龙提速前的速度是200米/分;④比赛全程为1 500米.其中正确的是( )
A. ①②③ B. ②③④
C. ①②④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】在棋盘中建立如图的直角坐标系,三颗棋子A,O,B的位置如图,它们分别是(﹣1,1),(0,0)和(1,0).

(1)如图2,添加棋子C,使A,O,B,C四颗棋子成为一个轴对称图形,请在图中画出该图形的对称轴;
(2)在其他格点位置添加一颗棋子P,使A,O,B,P四颗棋子成为一个轴对称图形,请直接写出棋子P的位置的坐标.(写出2个即可) -
科目: 来源: 题型:
查看答案和解析>>【题目】将连续正整数按以下规律排列,则位于第7行第7列的数x是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】根据2008~2012年杭州市实现地区生产总值(简称GDP,单位:亿元)统计图所提供的信息,下列判断正确的是( )
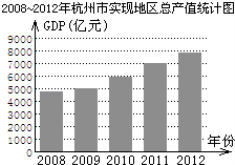
A.2010~2012年杭州市每年GDP增长率相同
B.2012年杭州市的GDP比2008年翻一番
C.2010年杭州市的GDP未达到5500亿元
D.2008~2012年杭州市的GDP逐年增长
相关试题

