【题目】如图1,二次函数y=ax2+bx+3 ![]() 经过点A(3,0),G(﹣1,0)两点.
经过点A(3,0),G(﹣1,0)两点.
(1)求这个二次函数的解析式;
(2)若点M时抛物线在第一象限图象上的一点,求△ABM面积的最大值;
(3)抛物线的对称轴交x轴于点P,过点E(0, ![]() )作x轴的平行线,交AB于点F,是否存在着点Q,使得△FEQ∽△BEP?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
)作x轴的平行线,交AB于点F,是否存在着点Q,使得△FEQ∽△BEP?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)解:将A、G点坐标代入函数解析式,得
![]() ,
,
解得 ![]() ,
,
抛物线的解析式为y=﹣ ![]() x2+2
x2+2 ![]() x+3
x+3 ![]()
(2)解:作ME⊥x轴交AB于E点,如图1
 ,
,
当x=0时,y=3 ![]() ,即B点坐标为(0,3
,即B点坐标为(0,3 ![]() )
)
直线AB的解析式为y=﹣ ![]() x+3
x+3 ![]() ,
,
设M(n,﹣ ![]() n2+2
n2+2 ![]() n+3
n+3 ![]() ),E(n,﹣
),E(n,﹣ ![]() n+3
n+3 ![]() ),
),
ME═﹣ ![]() n2+2
n2+2 ![]() n+3
n+3 ![]() ﹣(﹣
﹣(﹣ ![]() n+3
n+3 ![]() )=﹣
)=﹣ ![]() n2+5
n2+5 ![]() n,
n,
S△ABM= ![]() MExA=
MExA= ![]() (﹣
(﹣ ![]() n2+5
n2+5 ![]() n)×3=﹣
n)×3=﹣ ![]() (n﹣
(n﹣ ![]() )2+
)2+ ![]() ,
,
当n= ![]() 时,△ABM面积的最大值是
时,△ABM面积的最大值是 ![]()
(3)解:存在;理由如下:
OE= ![]() ,AP=2,OP=1,BE=3
,AP=2,OP=1,BE=3 ![]() ﹣
﹣ ![]() =
= ![]() ,
,
当y= ![]() 时,﹣
时,﹣ ![]() x+3
x+3 ![]() =
= ![]() ,解得x=
,解得x= ![]() ,即EF=
,即EF= ![]()
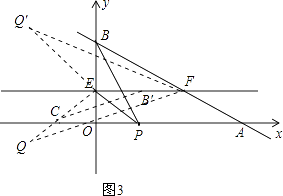
将△BEP绕点E顺时针方向旋转90°,得到△B'EC(如图3),
∵OB⊥EF,
∴点B'在直线EF上,
∵C点横坐标绝对值等于EO长度,C点纵坐标绝对值等于EO﹣PO长度,
∴C点坐标为(﹣ ![]() ,
, ![]() ﹣1),
﹣1),
过F作FQ∥B'C,交EC于点Q,
则△FEQ∽△B'EC,
由 ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
可得Q的坐标为(﹣ ![]() ,﹣
,﹣ ![]() );
);
根据对称性可得,Q关于直线EF的对称点Q'(﹣ ![]() ,
, ![]() )也符合条件.
)也符合条件.
【解析】(1)根据待定系数法,可得函数解析式;(2)根据平行于y轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得ME的长,根据三角形的面积,可得二次函数,根据二次函数的性质,可得答案.(3)即可确定△BEP,根据相似三角形的判定定理即可求得点Q的坐标,解题时要注意答案的不唯一性.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:(1)13=
 ×12×22;(2)13+23=
×12×22;(2)13+23= ×22×32;(3)13+23+33=
×22×32;(3)13+23+33= ×32×42;(4)13+23+33+43=
×32×42;(4)13+23+33+43= ×42×52;
×42×52;
根据上述等式的规律,解答下列问题:
(1)写出第5个等式:_____;
(2)写出第n个等式(用含有n的代数式表示);
(3)设s是正整数且s≥2,应用你发现的规律,化简:
 ×s2×(s+1)2﹣
×s2×(s+1)2﹣ ×(s﹣1)2×s2.
×(s﹣1)2×s2. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上三点M,O,N对应的数分别为﹣2,0,4,点P为数轴上任意一点,其对应的数为x.
(1)如果点P到点M点N的距离相等,则x= .
(2)数轴上是否存在点P,使点P到点M、点N的距离之和是10?若存在,求出x的值;若不存在,请说明理由.
(3)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,给出下列条件:①∠1=∠2;②∠3=∠4;③AD∥BC,且∠D=∠B;④AD∥BC,且∠BAD=∠BCD.其中,能推出AB∥DC的条件为( )
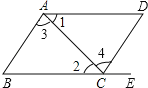
A.① B.② C.②③ D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一正方体,六个面上分别写有数字1,2,3,4,5,6,有三个人从不同的角度观察的结果如图.如果记6的对面的数字为a,2的对面的数字为b,那么a+b的值为( )
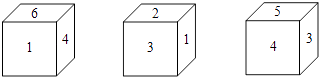
A.3
B.7
C.8
D.11 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点B、F、C、E在同一直线上,BF=CE,AB⊥BE,DE⊥BE,垂足分别为B、E,且AC=DF,连接AC、DF.求证:∠A=∠D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 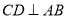 ,垂足为
,垂足为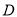 ,点
,点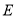 在
在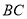 上,
上, 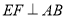 ,垂足为
,垂足为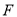 .
.(1)
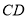 与
与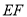 平行吗?为什么?
平行吗?为什么?(2)如果
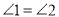 ,且
,且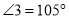 ,求
,求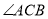 的度数.
的度数.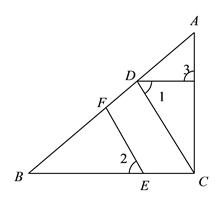
相关试题

