【题目】已知:如图,点B、F、C、E在同一直线上,BF=CE,AB⊥BE,DE⊥BE,垂足分别为B、E,且AC=DF,连接AC、DF.求证:∠A=∠D.

参考答案:
【答案】证明:∵BF=CE,
∴BF+FC=CE+FC.即BC=EF.
∵AB⊥BE,DE⊥BE,∴∠B=∠E=90°.
又AB=DE,∴△ABC≌△DEF,∴∠A=∠D.………………5分
【解析】
试题根据已知利用SAS判定△ABC≌△DEF,根据全等三角形的对应角相等即可得∠A=∠D.
试题解析::证明:∵BF=CE,
∴BF+FC=CE+FC.即BC=EF.
∵AB⊥BE,DE⊥BE,
∴∠B=∠E=90°.
在△ABC与△DEF中,
BC=EF
∠B=∠E
AB=DE
![]() ∴△ABC≌△DEF(SAS)
∴△ABC≌△DEF(SAS)
∴∠A=∠D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,给出下列条件:①∠1=∠2;②∠3=∠4;③AD∥BC,且∠D=∠B;④AD∥BC,且∠BAD=∠BCD.其中,能推出AB∥DC的条件为( )
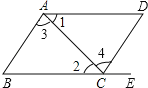
A.① B.② C.②③ D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,二次函数y=ax2+bx+3
 经过点A(3,0),G(﹣1,0)两点.
经过点A(3,0),G(﹣1,0)两点.
(1)求这个二次函数的解析式;
(2)若点M时抛物线在第一象限图象上的一点,求△ABM面积的最大值;
(3)抛物线的对称轴交x轴于点P,过点E(0, )作x轴的平行线,交AB于点F,是否存在着点Q,使得△FEQ∽△BEP?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
)作x轴的平行线,交AB于点F,是否存在着点Q,使得△FEQ∽△BEP?若存在,请直接写出点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一正方体,六个面上分别写有数字1,2,3,4,5,6,有三个人从不同的角度观察的结果如图.如果记6的对面的数字为a,2的对面的数字为b,那么a+b的值为( )
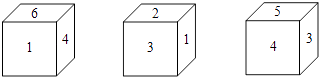
A.3
B.7
C.8
D.11 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
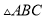 中,
中, 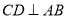 ,垂足为
,垂足为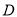 ,点
,点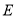 在
在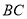 上,
上, 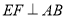 ,垂足为
,垂足为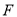 .
.(1)
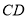 与
与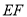 平行吗?为什么?
平行吗?为什么?(2)如果
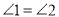 ,且
,且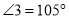 ,求
,求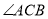 的度数.
的度数.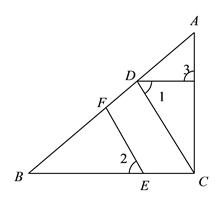
-
科目: 来源: 题型:
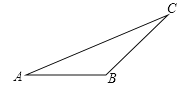
查看答案和解析>>【题目】画图并填空:
①画出图中△ABC的高AD(标注出点D的位置);
②画出把△ABC沿射线AD方向平移2cm后得到的△A1B1C1;
③根据“图形平移”的性质,得BB1=_____cm,AC与A1C1的位置关系是_____,数量关系是:________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.
解:因为:∠A=∠F,
所以:_____//______,
理由是:____________,
所以:∠____+∠_____=180°,
理由是:_______________,
因为:∠C=∠D,
所以∠D+∠DEC=180°,
理由是:_________________,
所以:______________________.

相关试题

