【题目】如图,二次函数的图象与x轴相交于点A(-3,0)B(-1,0),与y轴相交于点C(0,3),点P是该图象上的动点;一次函数y=kx-4k(k≠0)的图象过点P交x轴于点Q.

(1)求该二次函数的解析式;
(2)当点P的坐标为(-4,m)时,求证:∠OPC=∠AQC;
(3)点M、N分别在线段AQ、CQ上,点M以每秒3个单位长度的速度从点A向点Q运动,同时,点N以每秒1个单位长度的速度从点C向点Q运动,当点M、N中有一点到达Q点时,两点同时停止运动,设运动时间为t秒.
①连接AN,当△AMN的面积最大时,求t的值;
②线段PQ能否垂直平分线段MN?如果能,请求出此时直线PQ的函数关系式;如果不能请说明你的理由.
参考答案:
【答案】(1)y=![]() +4x+3;(2)证明过程见解析;(3)①、t=
+4x+3;(2)证明过程见解析;(3)①、t=![]() ;②、y=
;②、y=![]() .
.
【解析】
试题分析:(1)利用待定系数法求出函数解析式;(2)根据题意得出点P的坐标,从而得出PC∥x轴,根据一次函数的性质得出点Q的坐标和OQ的长度,从而得出四边形POQC为平行四边形,从而得出答案;(3)过点N作ND⊥x轴于点D,得到△QND∽△QCO,根据Rt△OCQ得出CQ的长度,根据相似得出ND的长度,然后得出S与t的函数关系式,求出最大值;假设PQ垂直平分线段MN,则QM=NQ,根据Rt△MND∽Rt△EQM,得出段E的坐标,然后求出直线QE的函数解析式.
试题解析:(1)抛物线的解析式为:y=![]() +4x+3
+4x+3
(2)当x=-4时,y=3,∴P(-4,3).
∵C(0,3),∴PC=4且PC∥x轴.
∵一次函数y=kx-4k(k≠0)的图象交x轴于点Q,当y=0时,x=4,
∴Q(4,0),即OQ=4.∴PC=OQ,
又∵PC∥x轴, ∴四边形POQC是平行四边形
∴∠OPC=∠AQC.
(3)①、过点N作ND⊥x轴于点D,则ND∥y轴. ∴△QND∽△QCO∴![]() ,
,
在Rt△OCQ中,CQ=![]() =5,
=5,
∴![]() ,
,
∴ND=![]() (5-t)
(5-t)
∴S△AMN=![]() AM·ND=
AM·ND=![]() ·3t·
·3t·![]() (5-t)=-
(5-t)=-![]()
∵0≤x≤![]()
∴当t=![]() 时,△AMN的面积最大
时,△AMN的面积最大
②、能.假设PQ垂直平分线段MN,则QM=NQ,
∴7-3t=5-t, ∴t=1.此时AM=3, 即点M与点O重合, QM=NQ=4.
如图,设PQ交y轴于点E
∵∠MND=90°-∠NMD=∠MQE,
∴Rt△MND∽Rt△EQM,
∴![]()
∵ND=![]() ,DQ=
,DQ=![]() ,
,
∴MD=![]() ,
,
∴MD=![]() .
.
∴E(0,![]() ),
),
∵Q(4,0),
∴直线QE为y=![]() . 即直线PQ为y=
. 即直线PQ为y=![]()

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各题中,计算结果正确的是( )
A. 19a2b﹣9ab2=10ab B. 3x+3y=6xy
C. 16y2﹣9y2=7 D. 3x﹣4x+5x=4x
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+3x+a=0有一个根为﹣2,则a=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
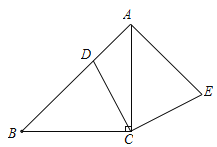
(1)求证:AB⊥AE.
(2)若点D为AB中点,求证:四边形ADCE是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为保证中、小学生每天锻炼一小时,某校开展了形式多样的体育活动项目,小明对某班同学参加锻炼的情况进行了统计,并绘制了下面的统计图①和图②.
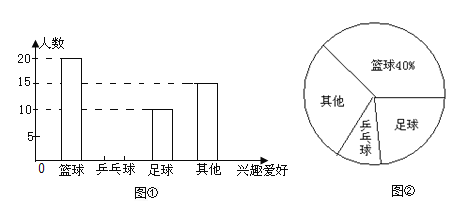
(1)请根据所给信息在图①中将表示“乒乓球”项目的图形补充完整;
(2)扇形统计图②中表示“足球”项目扇形的扇形圆心角的度数是 .
(3)该校中小学生共有2000名.请估计该校共有多少名同学参加“其他”项目的体育活动.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某班学生每天使用零花钱的情况,小红随机调查了该班15名同学,结果如下表:
每天使用零花钱(单位:元)
3
5
10
15
20
人数
2
6
3
3
1
则这15名同学每天使用零花钱的众数是( ).
A. 20元 B. 6元 C. 5元 D. 3元
-
科目: 来源: 题型:
查看答案和解析>>【题目】某家快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同,求该快递公司投递总件数的月平均增长率.
相关试题

