【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
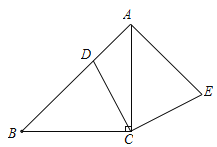
(1)求证:AB⊥AE.
(2)若点D为AB中点,求证:四边形ADCE是正方形.
参考答案:
【答案】(1)证明过程见解析;(2)证明过程见解析.
【解析】
试题分析:(1)根据∠ACB=∠DCE=90°可得∠BCD=∠ACE,从而得出△CBD和△CAE全等得出∠B=∠CAE,根据∠B+∠BAC=90°得出∠BAC+∠EAC=90°,即垂直;(2)根据D为中点得出∠ADC=90°,结合∠DCE=∠BAE=90°得出矩形,然后根据CD=CE得出正方形.
试题解析:(1)∵∠ACB=90°∴∠BCD+∠ACD=90°
∵∠DCE=90°∴∠ACD+∠ACE=90°
∴∠BCD=∠ACE
在△CBD与△CAE中,∵CB=CA, ∠BCD=∠ACE,CD=CE,∴△CBD≌△CAE,
∴∠B=∠CAE,
∵∠B+∠BAC=90°
∴∠BAC+∠EAC=90°
∴AB⊥AE
(2)∵点D为AB中点,∴∠ADC=90°
∵∠DCE=90°, ∠BAE=90°
∴四边形ADCE是矩形,
∴CD=CE,
∴四边形ADCE是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图为某地下停车库的出入口坡道示意图,其中AB∥MN,BD⊥AB,CE⊥AM.为张贴限高标志以确保车辆安全驶入,请你根据该图提供的数据计算CE.(参考数据:sin18°≈0.309,cos18°≈0.951,tan18°≈0.325,答案精确到0.1m)
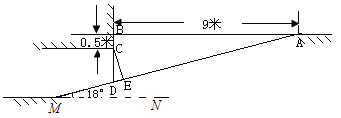
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各题中,计算结果正确的是( )
A. 19a2b﹣9ab2=10ab B. 3x+3y=6xy
C. 16y2﹣9y2=7 D. 3x﹣4x+5x=4x
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+3x+a=0有一个根为﹣2,则a=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数的图象与x轴相交于点A(-3,0)B(-1,0),与y轴相交于点C(0,3),点P是该图象上的动点;一次函数y=kx-4k(k≠0)的图象过点P交x轴于点Q.

(1)求该二次函数的解析式;
(2)当点P的坐标为(-4,m)时,求证:∠OPC=∠AQC;
(3)点M、N分别在线段AQ、CQ上,点M以每秒3个单位长度的速度从点A向点Q运动,同时,点N以每秒1个单位长度的速度从点C向点Q运动,当点M、N中有一点到达Q点时,两点同时停止运动,设运动时间为t秒.
①连接AN,当△AMN的面积最大时,求t的值;
②线段PQ能否垂直平分线段MN?如果能,请求出此时直线PQ的函数关系式;如果不能请说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为保证中、小学生每天锻炼一小时,某校开展了形式多样的体育活动项目,小明对某班同学参加锻炼的情况进行了统计,并绘制了下面的统计图①和图②.
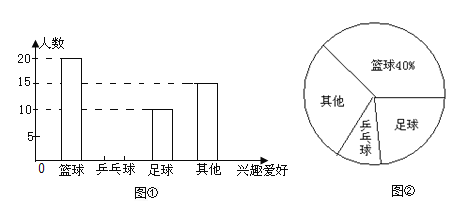
(1)请根据所给信息在图①中将表示“乒乓球”项目的图形补充完整;
(2)扇形统计图②中表示“足球”项目扇形的扇形圆心角的度数是 .
(3)该校中小学生共有2000名.请估计该校共有多少名同学参加“其他”项目的体育活动.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某班学生每天使用零花钱的情况,小红随机调查了该班15名同学,结果如下表:
每天使用零花钱(单位:元)
3
5
10
15
20
人数
2
6
3
3
1
则这15名同学每天使用零花钱的众数是( ).
A. 20元 B. 6元 C. 5元 D. 3元
相关试题

